Show that the rectangle of maximum perimeter which can be inscribed in a circle of radius $a$ is a square of side $\sqrt{2} a$ .

Video Solution

Text Solution

Verified by Experts

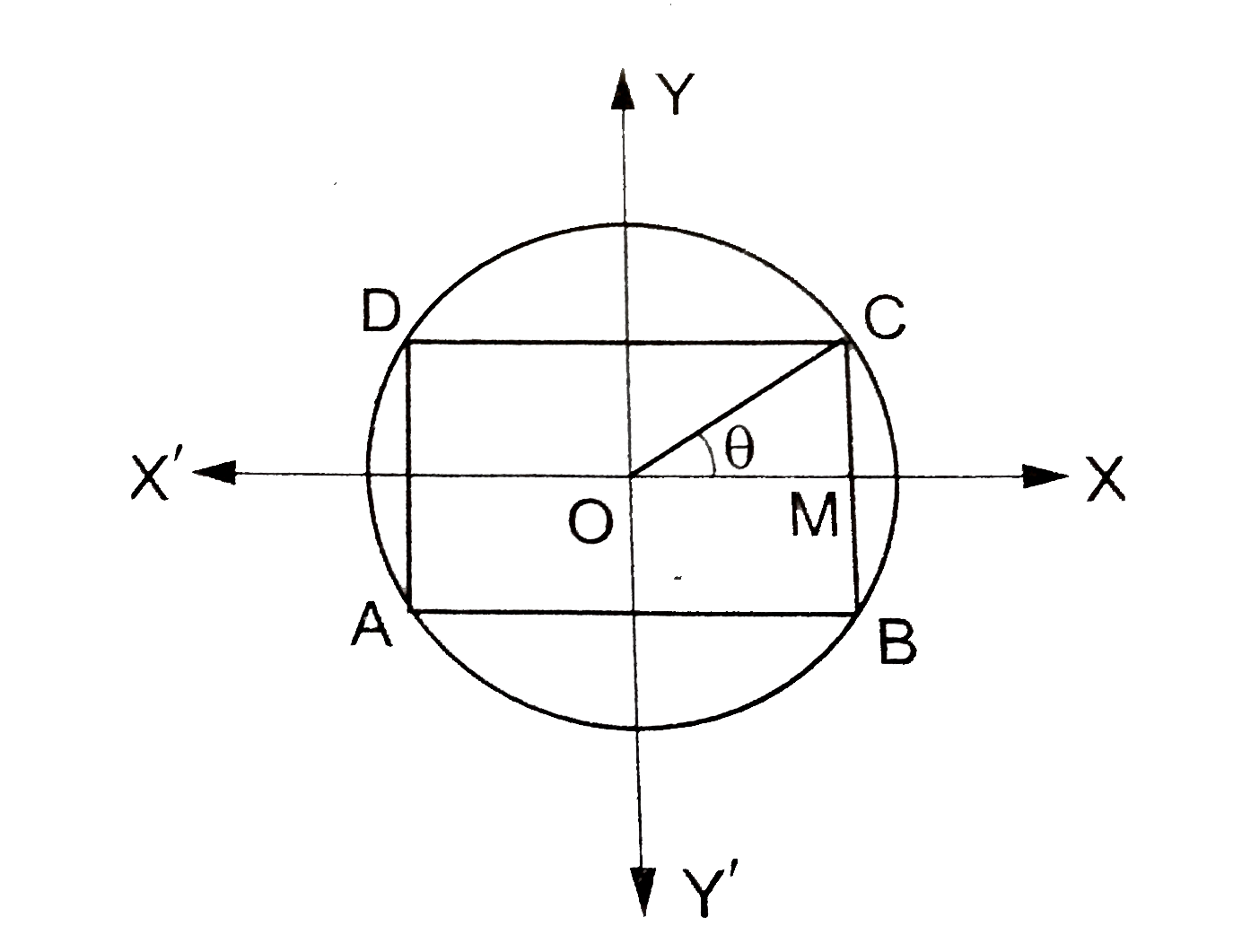
Let ABCD be the rectangle inscribed in a circle of radius a and with centre O. Join OC. Let $∠ C O X = θ$ . Then, the coordinates of C are $(a cos θ, a sin θ)$ .
$∴ O M = a cos θ and M C = a sin θ$
$B C = 2 M C = 2 a and C D = 2 O M = 2 a cos θ$
$∴ P = 2 a (cos θ + sin θ)$
So, $\frac{d P}{d θ} = 2 a (- sin θ + cos θ) and \frac{d^{2} P}{d θ^{2}} = - 2 a (cos θ + sin θ)$
$\frac{d P}{d θ} 0 \Rightarrow θ = \frac{π}{4}$ and at this value of $θ, \frac{d^{2} P}{d θ} < 0$
So, P is maximum at $θ = (π / 4)$
Then, $B C = \sqrt{2} a = C D$

Updated on:21/07/2023

The triangle of maximum area that can be inscribed in a given circle of radius 'r' is
AAn isoscles triangle with base equal to 2r
BAn equilateral of height $\frac{2 r}{3}$
Can equilateral trianlge having each of its side of length $\sqrt{3} r$
DA right angle triangle having two of its sides of length 2r and r.
The maximum area of rectangle, inscribed in a circle of radius 'r', is :
A $π r^{2}$
B $r^{2}$
C $2 r^{2}$
D $\frac{1}{4} π r^{2}$
Maximum area of a reactangle which can be inscribed in a circle of a given radius R is
A $\frac{π R^{2}}{3}$
B $\frac{3 R^{2}}{\sqrt{2}}$
C $2 R^{2}$
D $3 R^{2}$