A long cylinderical vessel is half filled with a liquid. When the vessel is rotated about its own vertical axis. The liquid rises up near the wall. If the radius of vessel is 5cm and its rotational speed is 2 rotatins per second, then the difference in the heights between the centre and the sides, in cm. will be :
Using v2=u2+2gh [∴u=0at(0,0)]
v2=2gy [∴v=ωx] 
⇒y=ω2x22g=(2×2π)2×(0.05)220=2cm
Topper's Solved these Questions
- CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSBOOK - DISHA PUBLICATIONCHAPTER - CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSEXERCISE - CHAPTER -10 (THERMAL PROPERTIES OF MATTER)
15 Videos
- CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSBOOK - DISHA PUBLICATIONCHAPTER - CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSEXERCISE - CHAPTER 11 (THERMODYNAMICS)
15 Videos
- CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSBOOK - DISHA PUBLICATIONCHAPTER - CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSEXERCISE - CHAPTER -7 (MECHANICAL PROPERTIES OF SOLIDS)
15 Videos
- ATOMSBOOK - DISHA PUBLICATIONCHAPTER - ATOMSEXERCISE - EXERCISE-2: CONCEPT APPLICATOR
30 Videos
- COMMUNICATION SYSTEM BOOK - DISHA PUBLICATIONCHAPTER - COMMUNICATION SYSTEM EXERCISE - EXERCISE-2 : Concept Applicator
30 Videos
Similar Questions
A cylindrical vessel containing a liquid is rotated about its axis so that the liquid rises at its sides as shown in the figure . The radius of vessel is 5 cm and the angular speed of rotation is ω rad s−1. The difference in the height , h ( in cm ) of liquid at the centre of vessel and at the side will be :
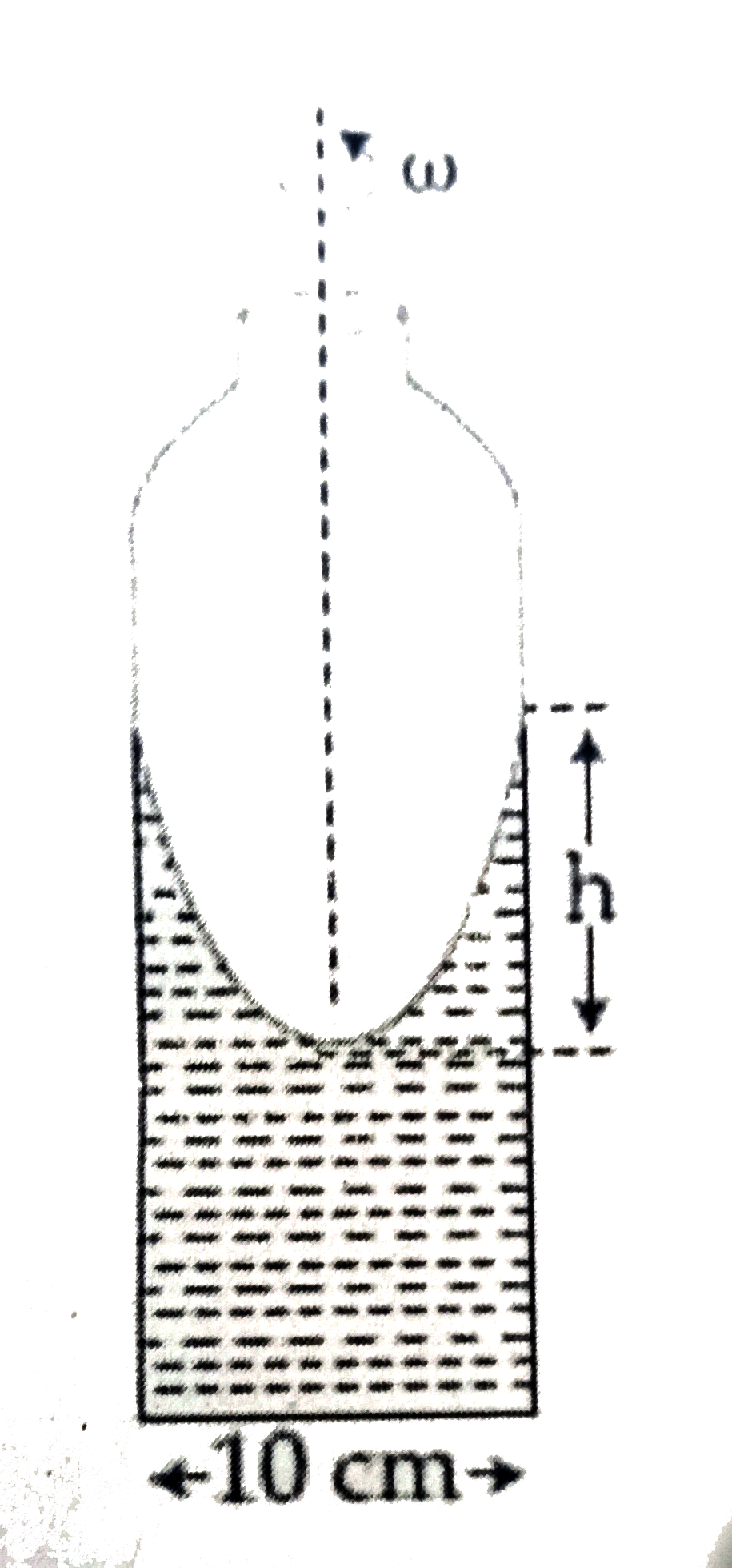
View SolutionA liquid is kept in a cylindrical vessel which is rotated along its axis. The liquid rises at the sides, if the radius of vessel is 0.05m and the speed of rotation is 2rev/s, find difference in the height of the liquid at the centre of the vessel and its sides.
View Solution
Knowledge Check
A cylindrical vessel partially filled with water is rotated about its vertical central axis. It’s surface will
ARise equallyBRise from the sidesCRise from the middleDLowered equallyA liquid is kept in a cylindrical vessel which is rotated along its axis. The liquid rises at the side. If the radius of the vessel is 5cm and the speed of rotation is 4rev/s, then the difference in the height of the liquid at the centre of the vessel and its sides is
A8cmB2cmC40cmD4cmA liquid is kept in a cylindrical vessel which is rotated along its axis. The liquid rises at the sides. If the radius of the vessel is r and the speed of revolution is n rotations/second, find the difference in height of the liquid at the centre of vessel and its sides.
Ah=2π2n2r2gBh=4π2n2r2gCh=π2r2n2gDh=π2r2n2g
The product of the numbers 5623 and 6 in the scale of eight is
View SolutionA liquid is kept in a cylindrical jar, which is rotated about the cylindrical axis. The liquid rises at its sides. The radius of the jar is r and speed of rotation is Ω the difference in height at the centre and the sides of the jar is
View SolutionA liquid is kept in a cylindrical vessel which is being rotated about a vertical axis through the centre of the circular base. If the radius of the vessel is r and angular velocity of rotation is ω, then the difference in the heights of the liquid at the centre of the vessel and the edge is.
View SolutionA liquid is kept in a cylindrical vessel which is being rotated about a vertical axis through the centre of the circular base. If the radius of the vessel is r and angular velocity of rotation is ω, then the difference in the heights of the liquid at the centre of the vessel and the edge is.
View SolutionA liquid kept in a cylindrical vessel of radius 0.3 m is rotated with a speed 2 r.p.s. The difference in the height of the liquid at the centre of the vessel and at it's sides it
View Solution