A composite wire of uniform diameter 3.0 mm consisting of a copper wire of length 2.2m and a steel wire of length 1.6m stretches under a load by 0.7 mm. Calculate the load, given that the Young's modulus for copper is 1.1×1011Pa and for steel is 2.0×1011Pa.
The extension ΔLcopper=Fl1AYc
=F×2.2π(0.003)2×1.1×1011
and ΔLsteel=Fl2AYs
=F×1.6π(0.003)2×2×1011
Given ΔLcopper+ΔLsteel=0.7×10−3
After simplifying above equations we get
F=176.8N
Topper's Solved these Questions
- CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSBOOK - DISHA PUBLICATIONCHAPTER - CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSEXERCISE - CHAPTER-9 (MECHANICAL PROPERTIES OF FLUIDS)
15 Videos
- CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSBOOK - DISHA PUBLICATIONCHAPTER - CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSEXERCISE - CHAPTER -10 (THERMAL PROPERTIES OF MATTER)
15 Videos
- CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSBOOK - DISHA PUBLICATIONCHAPTER - CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSEXERCISE - CHAPTER -7 (GRAVITATION)
15 Videos
- ATOMSBOOK - DISHA PUBLICATIONCHAPTER - ATOMSEXERCISE - EXERCISE-2: CONCEPT APPLICATOR
30 Videos
- COMMUNICATION SYSTEM BOOK - DISHA PUBLICATIONCHAPTER - COMMUNICATION SYSTEM EXERCISE - EXERCISE-2 : Concept Applicator
30 Videos
Similar Questions
A Copper wire of length 2.2m and a steel wire of length 1.6m, both of diameter 3.0mm are connected end to end. When stretched by a load, the net elongation is found to be 0.70 mm. Obtain the load applied . Young's modulus of copper is 1.1×1011Nm−2 and Young's modulus of steel is 2.0×1011Nm−2.
View SolutionA steel wire of length 4 m and diameter 5 mm is stretched by kg-wt. Find the increase in its length if the Young's modulus of steel wire is 2.4×1012dynecm−2
View Solution
Knowledge Check
A copper wire of length 4.0mm and area of cross-section 1.2cm2 is stretched with a force of 4.8×103N. If Young's modulus for copper is 1.2×1011N/m2, the increases in the length of the wire will be
A1.33mmB1.33cmC2.66mmD2.66cmA steel wire of length 5 m and area of cross-section 4mm2 is stretched by 2 mm by the application of a force. If young's modulus of steel is 2×1011N/m2, then the energy stored in the wire is
A0.64 JB0.16 JC0.32 JD1.28 J
Two wires of diameter 0.25cm, one made of steel and other made of brass, are loaded as shown in the figure. The unloaded length of the steel wire is 1.5m and that of brass is 1.0m. Young's modulus of steel is 2.0×1011Pa and that of brass is 1.0×1011 Pa. Compute the ratio of elongations of steel and brass wires. △lsteel△lbrass=?

View SolutionTwo wires of diameter 0.25 cm, one made of steel and the other made of brass are loaded as shown in figure. The unloaded length of steel wire is 1.5 m and that of brass wire is 1.0 m. Compute the elongations of the steel and the brass wires .Young's modulus of steel is 2.0×1011Pa and that of brass is 9.1×1011 Pa.
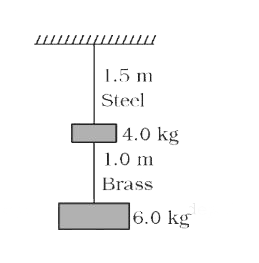
View Solution(a) A wire 4m long and 0.3 mm, calculate the potential energy stored in the wire.
Young's modulus for the material of wire is 2.0×1011N/m2.
View SolutionA steel wire of length 4 m and diameter 5 mm is strethed by 5 kg-wt. Find the increase in its length, if the Young's modulus of steel is 2×1012 dyne cm2
View SolutionA steel wire of length 4m and diameter 5mm is stretched by 5 kg-wt. Find the increase in its length , if the Young's modulus of steel wire is 2⋅4×10−12dyne/cm2
View SolutionA copper wire 2 m long and 0.5m in diameter supports a mass of 10kg It is stretched by 2.38 mm . Calculate the Young's modulus of the wire.
View Solution
