Two sides of a rhombus ABCD are parallel to the lines y = x + 2 and y = 7x + 3 If the diagonals of the rhombus intersect at the point (1, 2) and the vertex A is on the y-axis, then vertex A can be
Let the coordinates of A be (0,α). Since, the sides AB and AD are parallel to the lines y=x+2 and y=7x+3, respectively.
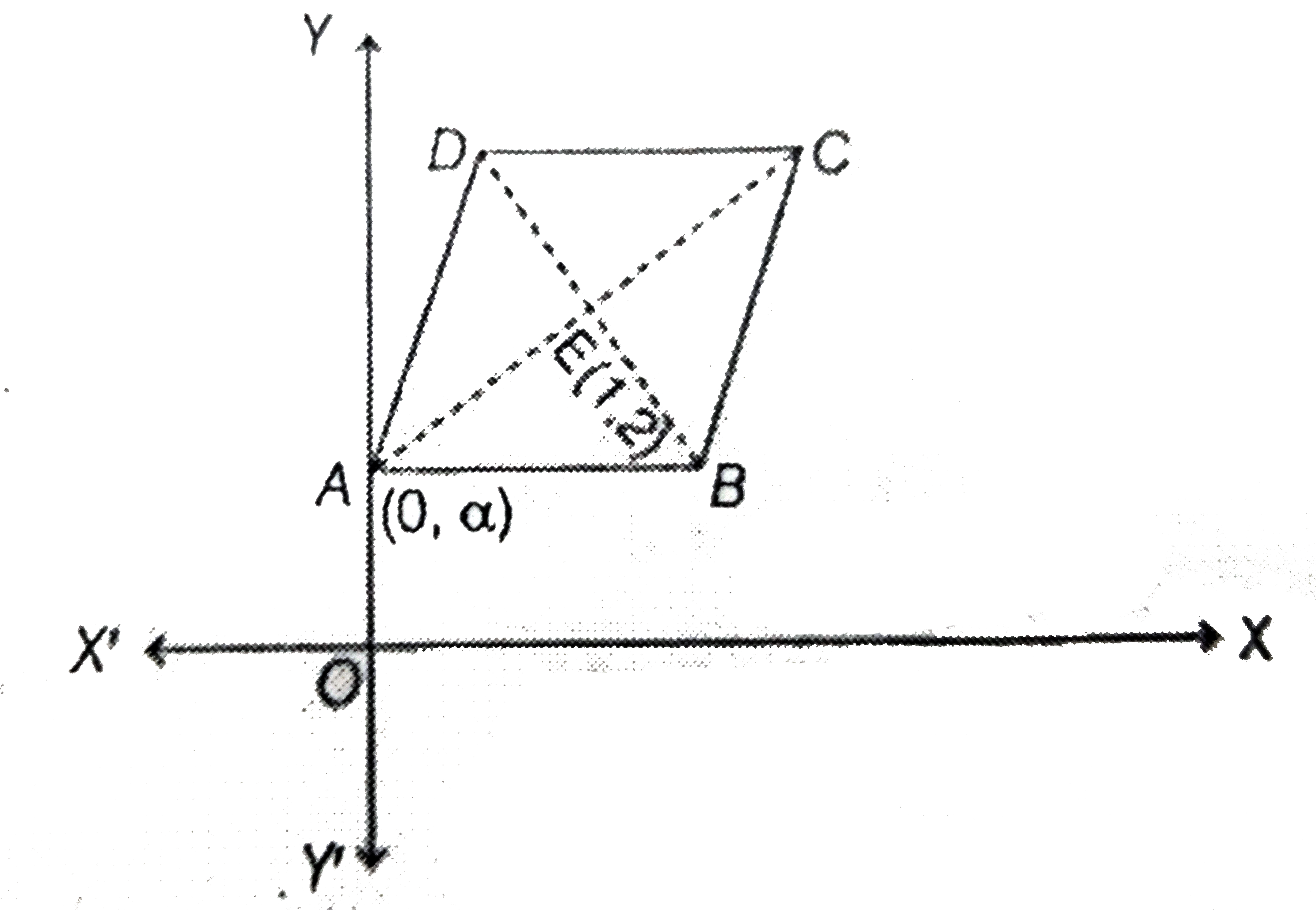
∴ The diagonal AC is parallel to the bisector of the angle between these two lines. The equation of the bisectors are given by
x−y+2√2=±7x−y+3√50
⇒5(x−y+2)=±(7x−y+3)
⇒2x+4y−7=0 and 12x−6y+13=0
Thus, the diagonals of the rhombus are parallel to the lines 2x+4y−7=0 and 12x−6y+13=0
∴ Slope of AE=−24 or 126
⇒2−α1−0=−12 or 2−α1−0=2
⇒α=52 or α=0
Hence, the coordinates are (0,5/2) or (0,0).
Topper's Solved these Questions
- STRAIGHT LINE AND PAIR OF STRAIGHT LINESBook:IIT JEE PREVIOUS YEARChapter:STRAIGHT LINE AND PAIR OF STRAIGHT LINESExercise:VARIOUS FORMS OF STRAIGHT LINE (Integer Answer Type Question)
Explore 1 Video
- STRAIGHT LINE AND PAIR OF STRAIGHT LINESBook:IIT JEE PREVIOUS YEARChapter:STRAIGHT LINE AND PAIR OF STRAIGHT LINESExercise:ANGLE BETWEEN STRAIGHT LINE AND EQUATION OF ANGLE BISECTOR (Objective Questions II) (One or more than one correct option)
Explore 3 Videos
- STRAIGHT LINE AND PAIR OF STRAIGHT LINESBook:IIT JEE PREVIOUS YEARChapter:STRAIGHT LINE AND PAIR OF STRAIGHT LINESExercise:VARIOUS FORMS OF STRAIGHT LINE (True/False)
Explore 3 Videos
- SOLVED PAPER 2019Book:IIT JEE PREVIOUS YEARChapter:SOLVED PAPER 2019Exercise:Paper -2 section-3
Explore 4 Videos
- THEORY OF EQUATIONSBook:IIT JEE PREVIOUS YEARChapter:THEORY OF EQUATIONSExercise:SOME SPECIAL FORMS
Explore 18 Videos
Similar Questions
Two sides of a rhombus ABCD are parallel to the lines y = x + 2 and y = 7x + 3. If the diagonals of the rhombus intersect at the point (1, 2) and the vertex A is on the y-axis, find the possible coordinates of A. x – y – 1 = 0 are the equations of two internal bisectors of its angles.
View SolutionThe sides of a rhombus are parallel to the lines x+y−1=0 and 7x−y−5=0. It is given that the diagonals of the rhombus intersect at (1, 3) and one vertex, A of the rhombus lies on the line y=2x . Then the coordinates of vertex A are (a)(85,165) (b) (715,1415) (c)(65,125) (d) (415,815)
View Solution
Knowledge Check
The sides of a rhombus ABCD are parallel to the lines x−y+2=0 and 7x−y+3=0, If the diagonals of the rhombus intersect at P(1,2) and the vertex A (different from the origin) is on the y-axis then the ordinate of A is:
A2B52C74D72Two sides of a rhombus are along the lines,x−y+1=0 and 7x−y−5=0 . If its diagonals intersect at (−1,−2) , then which one of the following is a vertex of this rhombus ?
A(-3, -8)B(13,−83)C((−103,−73)D(-3, -9)
Two sides of a Rhombus ABCD are parallel to the lines x−y=5 and 7x−y=3. The diagonals intersect at (2,1) then the equations of the diagonals are
View SolutionThe sides of a rhombus are parallel to y=2x+3and2y=x+5 . The diagonals of the rhombus intersect at (1, 2). If one vertex of the rhombus lies on the y-axis then possible values of the ordinates of this vertex are 1 (b) 2 (c) 3 (d) 4
View SolutionIf the diagonals of a rhombus are x and y, the what is its area ?
View SolutionA rhombus has two of its sides parallel to the lines y=2x+3andy=7x+2. If the diagonals cut at (1, 2) and one vertex is on the y-axis, find the possible values of the ordinate of that vertex.
View SolutionSides of a rhombus are parallel to x+y=0,7x=y. Its centre is (2,7), then its diagonals are
View SolutionTwo sides of a parallelogram are along the lines x+y=3 and x−y+3=0 .If its diagonal intersect at (2,4) then one of its vertex is
View Solution

