A rectangle PQRS has its side PQ parallel to the line $y = m x$ and vertices $P, Q$ , and $S$ on the lines $y = a, x = b$ ,and $x = - b$ , respectively. Find the locus of the vertex $R$ .

Video Solution

Text Solution

Verified by Experts

Let the coordinates of $Q$ be $(b, α)$ and that of $S$ be $(- b, β)$ . Suppose , $P R$ and $S Q$ meet in $G$ . Since, $G$ is mid-point of $S Q$ , its $x$ -coordinate must be $0$ . Let the coordinates of $R$ be $(h, k)$ .
Since $G$ , is mid point of $P R$ , the $x$ -coordinate at $P$ must be $- h$ and as $P$ lies on the line $y = a$ , the coordinates of $P$ are $(- h, a)$ . Since , $P Q$ is parallel to $y = m x$ , slope of $P Q = m$
$\Rightarrow \frac{α - a}{b + h} = m$ ......... $(i)$
Again $R Q ⊥ P Q$

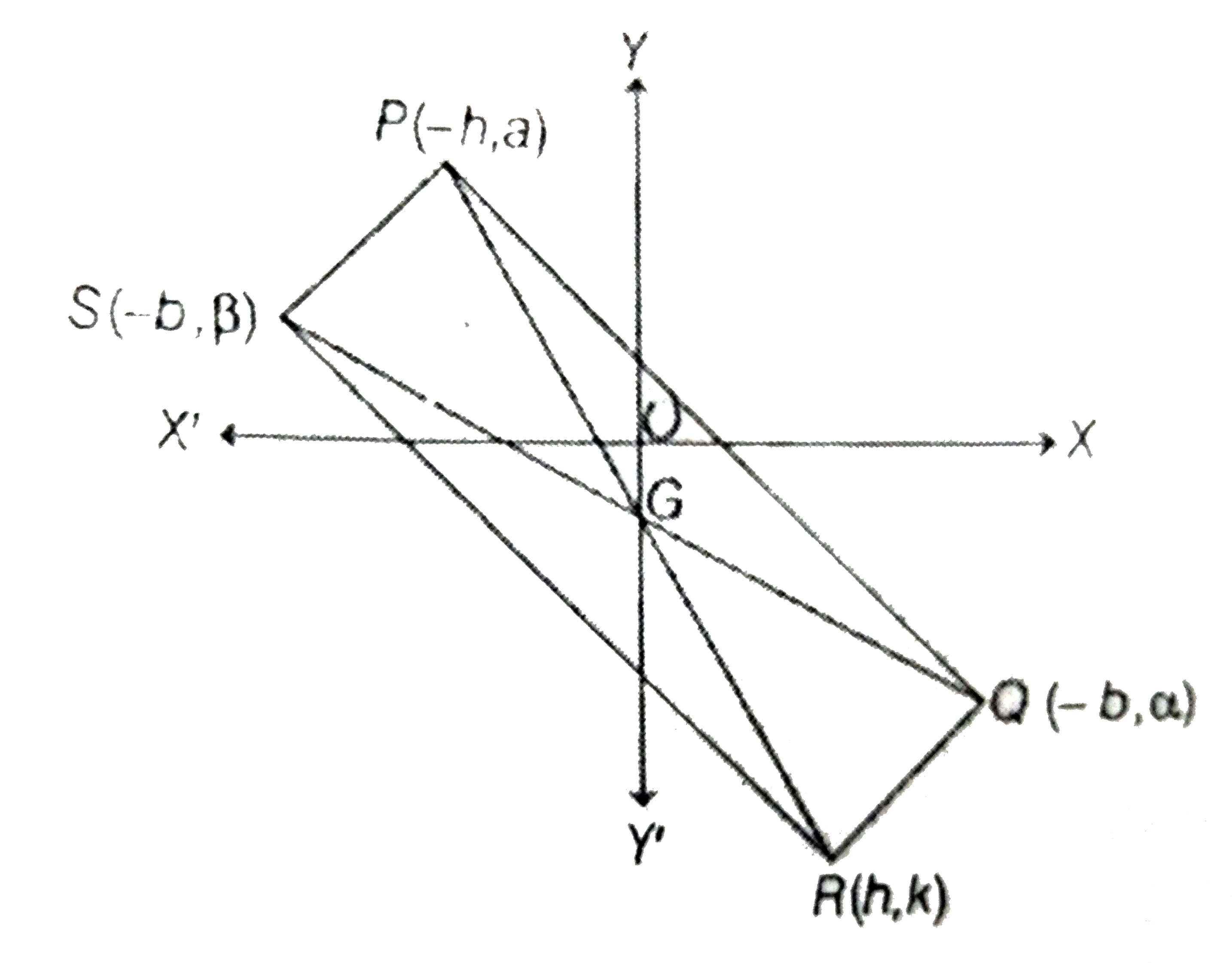
Slope of $R Q = - \frac{1}{m} \Rightarrow \frac{k - α}{h - b} = - \frac{1}{m}$ ......... $(i i)$
From Eq. $(i)$ , we get
$α - a = m (b + h)$
$\Rightarrow α = a + m (b + h)$ .......... $(i i i)$
and from Eq. $(i i)$ , we get
$k - α = - \frac{1}{m} (h - b)$
$\Rightarrow α = k + \frac{1}{m} (h - b)$ ....... $(i v)$
From Eqs. $(i i i)$ and $(i v)$ , we get
$a + m (b + h) = k + \frac{1}{m} (h - b)$
$\Rightarrow a m + m^{2} (b + h) = k m + (h - b)$
$\Rightarrow (m^{2} - 1) h - m k + b (m^{2} + 1) + a m = 0$
Hence, the locus of vertex is
$(m^{2} - 1) x - m y + b (m^{2} + 1) + a m = 0$

Updated on:21/07/2023

A rectangle ABCD has its side AB parallel to line y =x and vertices A,B and D lie on y = 1, x = 2 and x = -2, respectively. Locus of vertex 'C' is
Ax = 5
Bx-y = 5
Cy = 5
Dx+y = 5
A rectangle ABCD has its side AB parallel to line y =x and vertices A,B and D lie on y = 1, x = 2 and x = -2, respectively. Locus of vertex 'C' is
Ax = 5
Bx-y = 5
Cy = 5
Dx+y = 5
The image of P(a,b) in the line y=−x is Q and the image of Q in the line y=x is R. Then the midpoint of PR is
A $(a + b, b + a)$
B $((a + b) / 2, (b + 2) / 2)$
C $(a - b, b - a)$
D $(0, 0)$