A line through $A (- 5, - 4)$ meets the lines $x + 3 y + 2 = 0, 2 x + y + 4 = 0 a n d x - y - 5 = 0$ at the points $B, C a n d D$ rspectively, if ${(\frac{15}{A B})}^{2} + {(\frac{10}{A C})}^{2} = {(\frac{6}{A D})}^{2}$ find the equation of the line.

Video Solution

Text Solution

Verified by Experts

Let equation of line $A C$ is
$\frac{y + 4}{sin θ} = \frac{x + 5}{cos θ} = r$
Let line $A E$ make angle $θ$ with $X$ - axis and intersects $x + 3 y + 2 = 0$ at $B$ at a distance $r_{1}$ and line $2 x + y + 4 = 0$ at $C$ at a distance $r_{2}$ and line $x - y - 5 = 0$ at $D$ at a distance $r_{3}$ .
$∴ A B = r_{1}$ , $A C = r_{2}$ , $A D = r_{3}$ .
$r_{1} = \frac{- 5 - 3 \times 4 + 2}{1 \cdot cos θ + 3 \cdot sin θ} [∵ r = - \frac{I'}{(α cos θ + b sin θ)}]$
$\Rightarrow r_{1} = \frac{15}{cos θ + 3 sin θ}$ ...... $(i)$
Similarly, $r_{2} = - \frac{2 \times (- 5) + 1 (- 4) + 4}{2 cos θ + 1 \cdot sin θ}$

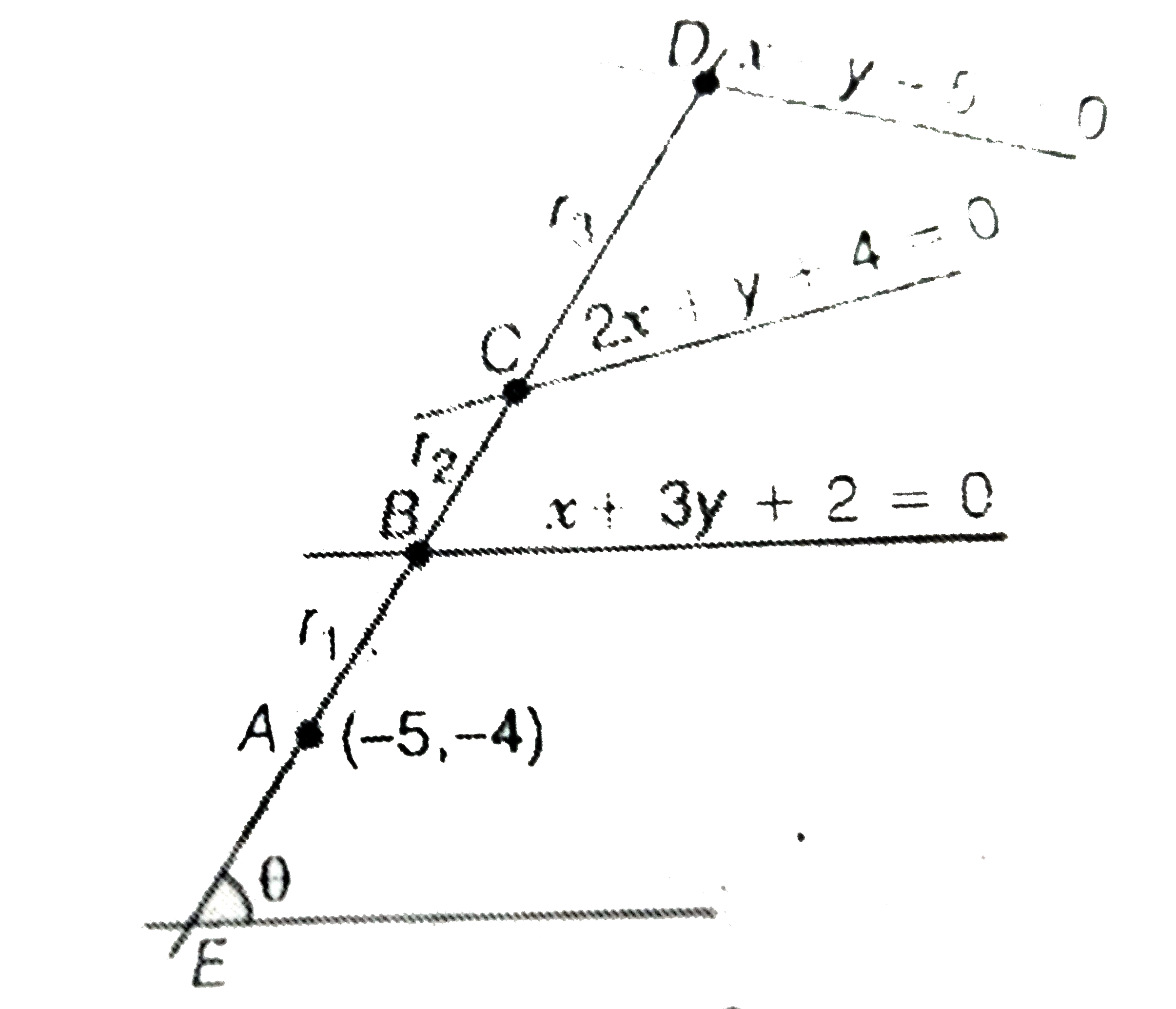
$\Rightarrow r_{2} = \frac{10}{2 cos θ + sin θ}$ ..... $(i i)$
and $r_{3} = - \frac{- 5 \times 1 - 4 (- 1) - 5}{cos θ - sin θ}$
$\Rightarrow r_{3} = \frac{6}{cos θ - sin θ}$ ......... $(i i i)$
But it is given that,
${(\frac{15}{A B})}^{2} + {(\frac{10}{A C})}^{2} = {(\frac{6}{A D})}^{2}$
$\Rightarrow {(\frac{15}{r_{1}})}^{2} + {(\frac{10}{r_{2}})}^{2} = {(\frac{6}{r_{3}})}^{2}$
$\Rightarrow {(cos θ + 3 sin θ)}^{2} + {(2 cos + sin θ)}^{2} = {(cos θ - sin θ)}^{2}$ [from Eqs. $(i)$ , $(i i)$ and $(i i i)$ ]
$\Rightarrow {cos}^{2} θ + 9 {sin}^{2} θ + 6 cos θ sin θ + 4 {cos}^{2} θ + {sin}^{2} θ + 4 cos θ sin θ = {cos}^{2} θ + {sin}^{2} θ - 2 cos θ sin θ$
$\Rightarrow 4 {cos}^{2} θ + 9 {sin}^{2} θ + 12 sin θ cos θ = 0$
$\Rightarrow {(2 cos θ + 3 sin θ)}^{2} = 0$
$\Rightarrow 2 cos θ + 3 sin θ = 0$
$\Rightarrow cos θ = - (3 / 2) sin θ$
Onsubsituting this in equation of $A C$ , we get
$\frac{y + 4}{sin θ} = \frac{x + 5}{- \frac{3}{2} sin θ}$
$\Rightarrow - 3 (y + 4) = 2 (x + 5)$
$\Rightarrow - 3 y - 12 = 2 x + 10$
$\Rightarrow 2 x + 3 y + 22 = 0$
which is the equation of required straight line.

Updated on:21/07/2023