The equations of the perpendicular bisectors of the sides $A B a n d A C$ of triangle $A B C$ are $x - y + 5 = 0$ and $x + 2 y = 0$ , respectively. If the point $A$ is $(1, - 2)$ , then find the equation of the line $B C .$

Video Solution

Text Solution

Verified by Experts

Let the coordinates of $B$ and $C$ be $(x_{1}, y_{1})$ and $(x_{2}, y_{2})$ respectively. Let $m_{1}$ and $m_{2}$ be the slopes of $A B$ and $A C$ , respectively. Then,

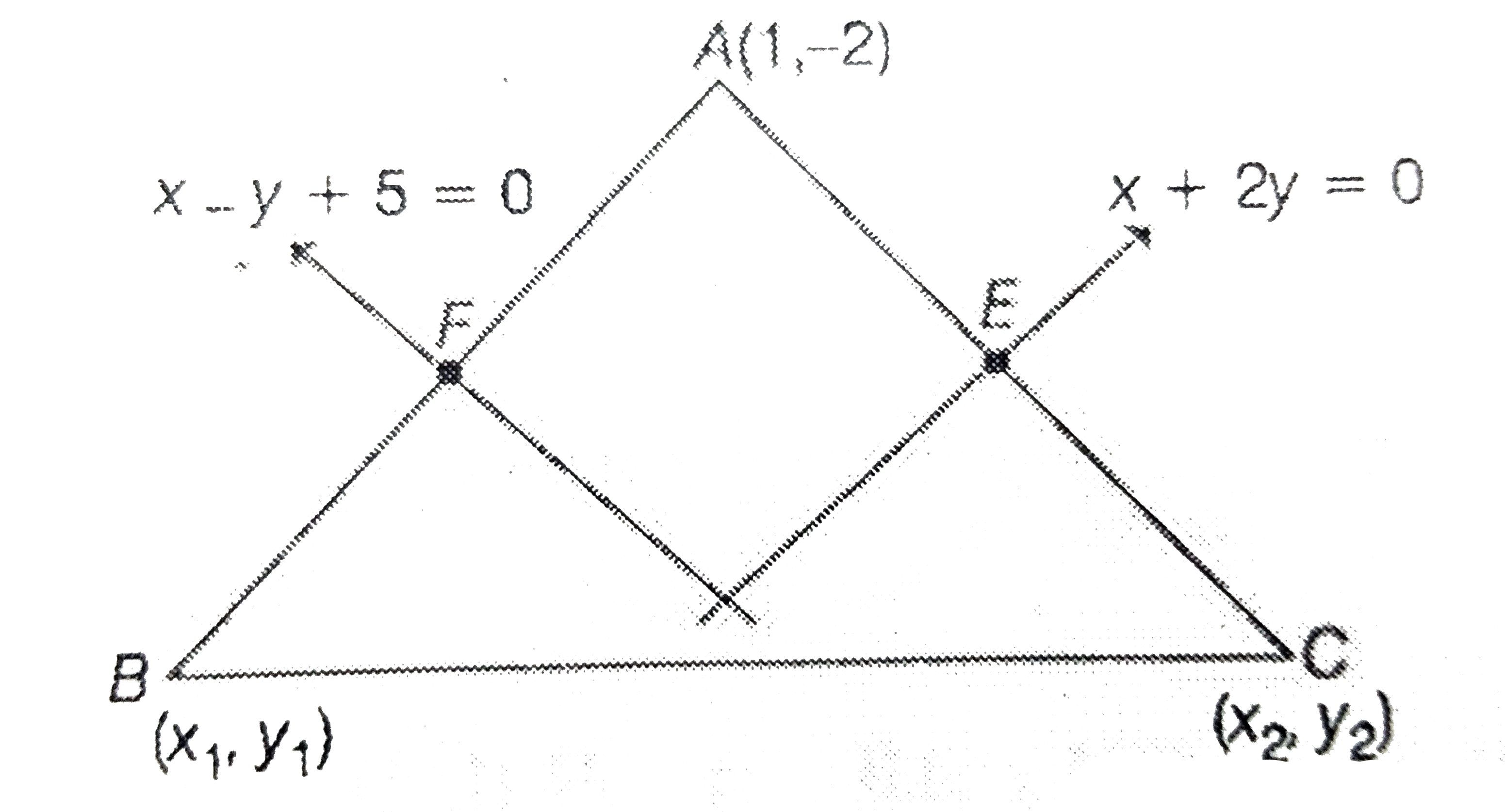
$m_{1} = slope of A B = \frac{y_{1} + 2}{x_{1} - 1}$
and $m_{2} = slope of A C = \frac{y_{2} + 2}{x_{2} - 1}$
Let $F$ and $E$ be the mid point of $A B$ and $A C$ , respectively.
Then, the coordinates of $E$ and $F$ are
$E (\frac{x_{1} + 1}{2}, \frac{y_{2} - 2}{2})$ and $F (\frac{x_{1} + 1}{2}, \frac{y_{2} - 2}{2})$ , respectively.
Now, $F$ lies on $x - y + 5 = 0$
$\Rightarrow \frac{x_{1} + 1}{2} - \frac{y_{1} - 2}{2} = - 5$
$\Rightarrow x_{1} - y_{1} + 13 = 0$ ......... $(i)$
Since, $A B$ is perpendicular to $x - y + 5 = 0$
$∴ (slope of A B) \cdot (slope of x - y + 5 = 0) = - 1$
$\Rightarrow \frac{y_{1} + 2}{x_{1} - 1} \cdot (1) = - 1$
$\Rightarrow y_{1} + 2 = - x_{1} + 1$
$\Rightarrow x_{1} + y_{1} + 1 = 0$ ........ $(i i)$
On solving Eqs. $(i)$ and $(i i)$ , we get
$x_{1} = - 7$ , $y_{1} = 6$
So, the coordinates of $B$ are $(- 7, 6)$ .
Now, $E$ lies on $x + 2 y = 0$
$∴ \frac{x_{2} + 1}{2} + 2 (\frac{y_{2} - 2}{2}) = 0$
$\Rightarrow x_{2} + 2 y_{2} - 3 = 0$ ........ $(i i i)$
Since, $A C$ is perpendicular to $x + 2 y = 0$
$∴ (slope of A C) \cdot (s l o p e o f x + 2 y = 0) = - 1$
$\Rightarrow \frac{y_{2} + 2}{x_{2} - 1} \cdot (- \frac{1}{2}) = - 1$
$\Rightarrow 2 x_{2} - y_{2} = 4$ .... $(i v)$
On solving Eqs. $(i i i)$ and $(i v)$ , we get
$x_{2} = \frac{11}{5}$ and $y_{2} = \frac{2}{5}$
So, the coordinates of $C$ are $(\frac{11}{5}, \frac{2}{5})$
Thus, the equation of $B C$ is
$y - 6 = \frac{2 / 5 - 6}{11 / 5 + 7} (x + 7)$
$\Rightarrow - 23 (y - 6) = 14 (x + 7)$
$\Rightarrow 14 x + 23 y - 40 = 0$

Updated on:21/07/2023

The equations of perpendicular bisectors of the sides AB and AC of a triangle ABC are $x - y + 5 = 0$ and $x + 2 y = 0$ respectively
If the point A is (1,-2) the equation of the line BC is
A $23 x + 4 y - 40 = 0$
B $23 x + 14 y + 40 = 0$
C $14 x + 23 y - 40 = 0$
D $14 x + 23 y + 40 = 0$
The equations of perpendicular bisectors of the sides AB and AC of a $Δ A B C$ are $x - y + 5 = 0$ and $x + 2 y = 0$ , respectively. If the point A is (1, - 2) the equation of the line BC is
A $23 x + 14 - 40 = 0$
B $23 + 14 y + 40 = 0$
C $14 x + 23 y - 40 = 0$
D $14 x + 23 y + 40 = 0$
The equations of perpendicular bisectors of the sides AB and AC of a $Δ A B C$ are $x - y + 5 = 0$ and $x + 2 y = 0$ , respectively. If the point A is (1, - 2) the equation of the line BC is
A $23 x + 14 y - 40$
B $23 x + 14 y + 40 = 0$
C $14 x + 23 y - 40 = 0$
D $14 x + 23 y + 40 = 0$