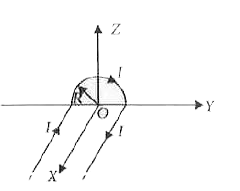
A wire is bent into three circular segment of radius r=10cm as shown in. Each segment is a quadrant of a circle ab lying in the x−y plane, bc lying in the y−z plane and ca lying in the z−x plane.
(a) if a magnetic field B points in the positive x direction, what is the magnitude of the emf developed in the wire when B increases at the rate of 3mTs−1?
(b) What is the direction of the current in the segment bc.
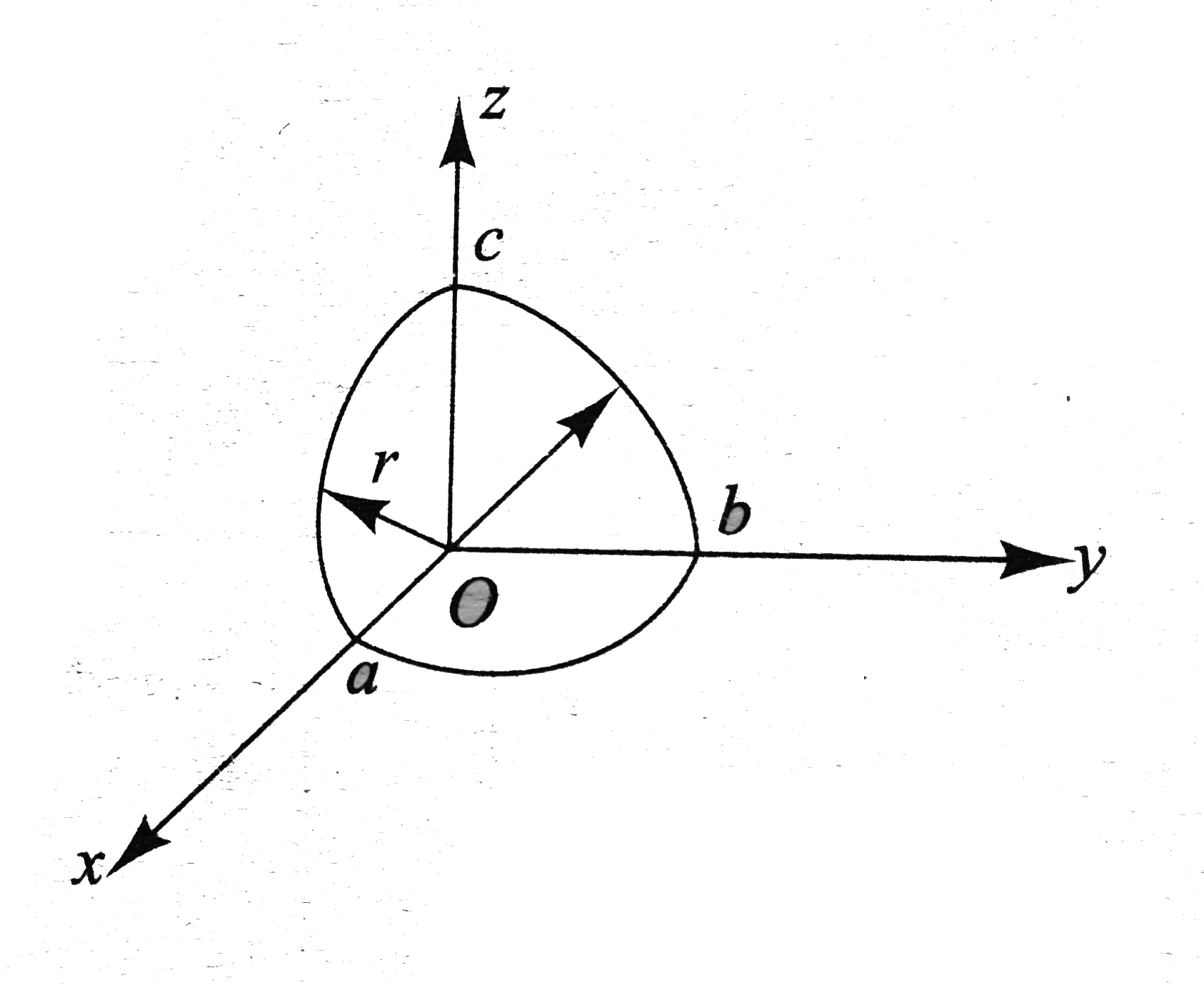
(a) 2.4×10−5 V, (b) the current in segment be flows from c to b (following Lenz.s law)
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBook:RESNICK AND HALLIDAYChapter:ELECTROMAGNETIC INDUCTIONExercise:PRACTICE QUESTIONS (Single Correct Choice Type)
Explore 45 Videos
- ELECTROMAGNETIC INDUCTIONBook:RESNICK AND HALLIDAYChapter:ELECTROMAGNETIC INDUCTIONExercise:PRACTICE QUESTIONS (More than One Correct Choice Type)
Explore 13 Videos
- ELECTROMAGNETIC INDUCTIONBook:RESNICK AND HALLIDAYChapter:ELECTROMAGNETIC INDUCTIONExercise:CHECKPOINTS
Explore 9 Videos
- ELECTRIC POTENTIALBook:RESNICK AND HALLIDAYChapter:ELECTRIC POTENTIALExercise:(PRACTICE QUESTIONS) Integer Type
Explore 1 Video
- ELECTROMAGNETIC OSCILLATIONS AND ALTERNATING CURRENT Book:RESNICK AND HALLIDAYChapter:ELECTROMAGNETIC OSCILLATIONS AND ALTERNATING CURRENT Exercise:Practice Questions (Integer)
Explore 7 Videos
Similar Questions
A wire is bent into three circular segment og radius r=10cm as shown in. Each segment is a quardrant of a circle ab lyinf in rthe x−y plane, bc lying in the y−z plane and ca lying in the z−x plane.
(a) if a magnetic field B points in the positive x direction, what is the magnitude of the emf developed in the wire when B increases at the rate of 3mTs−1?
(b) What is the direction of teh current in the segment bc.

View SolutionA wire, carrying a current i, is kept in the x−y plane along the curve y=Asin(2πλx). A magnetic field B exista in the z-direction. Find the magnitude of the magnetic force on the portion of the wire between x=0andx=λ.
View Solution
Knowledge Check
A wire is bent into three segments each of radius r. Each segment is a quardant of a circle. The first segment lies in X−Y plane, the second in the Y−Z plane and third in XZ plane. If a current i flows in the wire then net dipole moment of wire is:
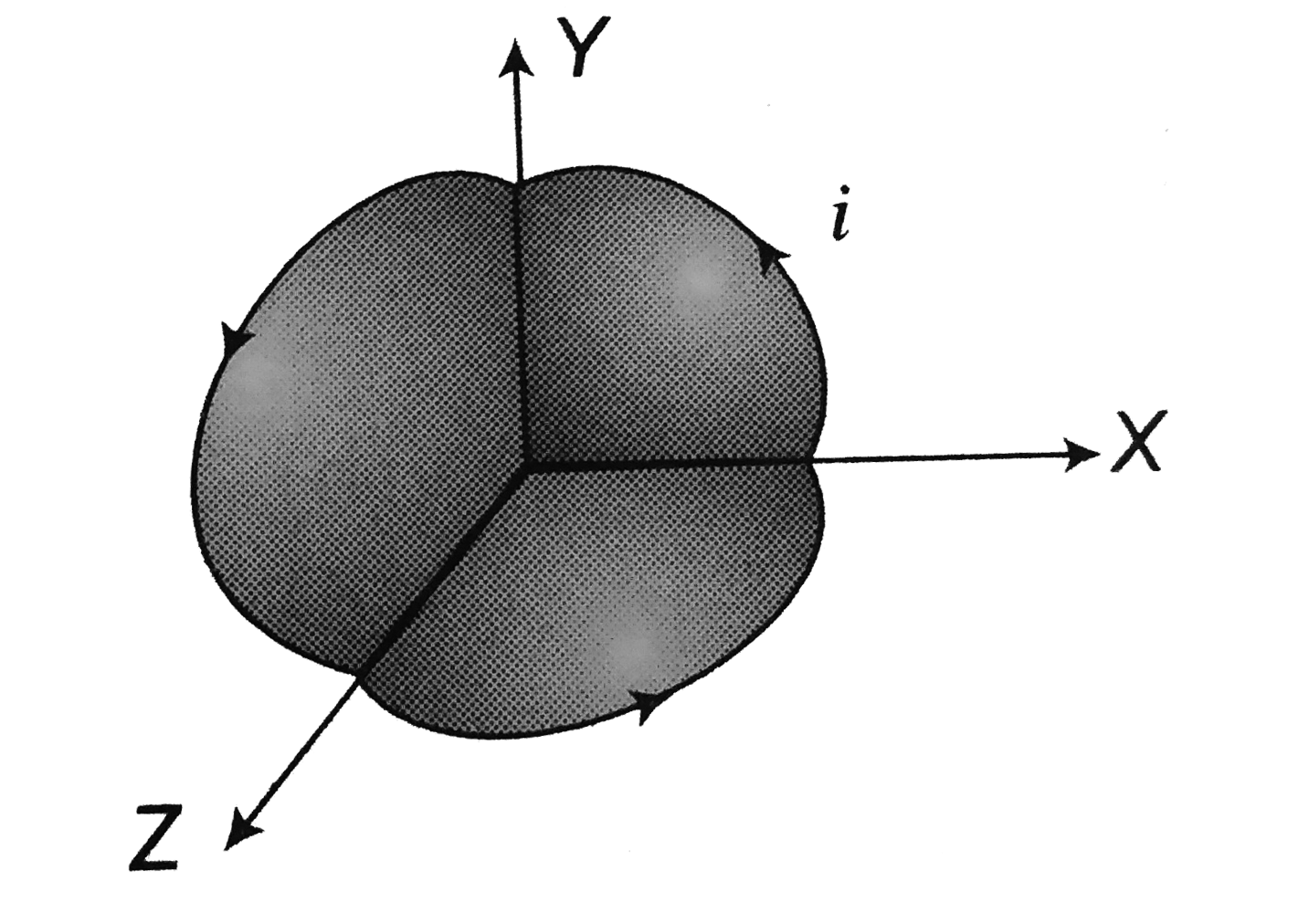 Aπa2i(ˆi+ˆj)Bπa24i(ˆi+ˆj+ˆk)Cπa22i(ˆj+ˆk)Dπa22i(ˆi+ˆj+ˆk)
Aπa2i(ˆi+ˆj)Bπa24i(ˆi+ˆj+ˆk)Cπa22i(ˆj+ˆk)Dπa22i(ˆi+ˆj+ˆk)A wire ABCDEF (with each side of length L) bent as shown in figure and carrying a current / is placed in a uniform magnetic field B parallel to the positive y direction. The force experienced by the wire in the z direction is
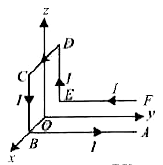 A2BILˆkBBIL2ˆkCBILˆkDBIL4ˆk
A2BILˆkBBIL2ˆkCBILˆkDBIL4ˆkA wire carrying current I has the shape as shown in the adjoining figure. Linear parts of the wire are very long and parallel to X-axis while semicicular portion of radius R is lying in Y−Z plane. Magnetic field at point O is
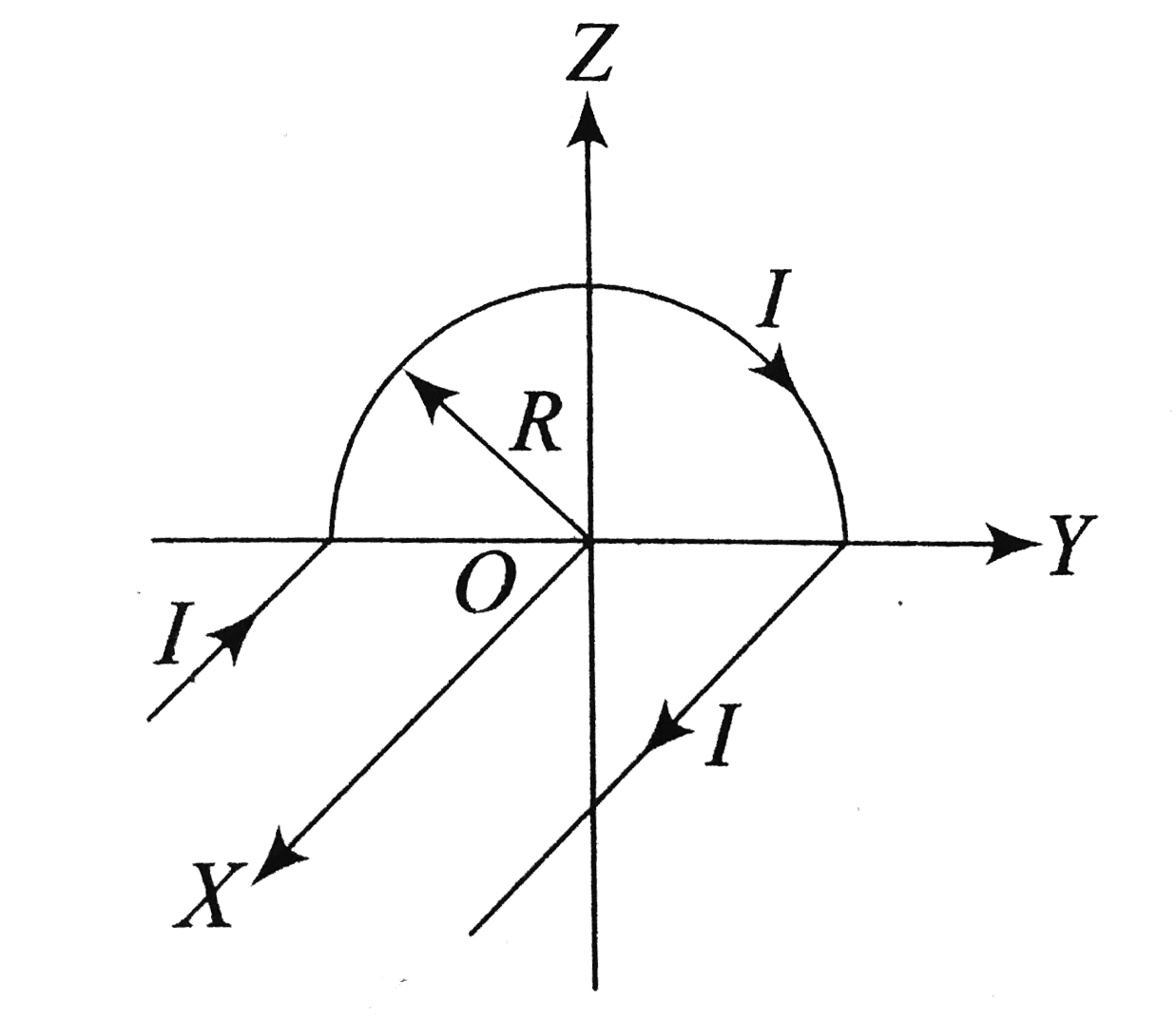 A→B=−μ04πIR(μˆi×2ˆk)B→B=−μ04πIR(μˆi+2ˆk)C→B=−μ04πIR(πˆi−2ˆk)D→B=−μ04πIR(πˆi+2ˆk)
A→B=−μ04πIR(μˆi×2ˆk)B→B=−μ04πIR(μˆi+2ˆk)C→B=−μ04πIR(πˆi−2ˆk)D→B=−μ04πIR(πˆi+2ˆk)
What is the y intercept of the plane x-5y+7z=10
View SolutionA wire, carriying a current I is kept in the x-y plame the curve y -(2 cm) Asin(2πλx).Amag≠ticfieldB∃∈thez−direction.F∈dthemagnitudeofthemag≠ticforceontheportionofthewirebetweenz−−0andx=lambda//2
View SolutionIn Fig, find the magnetic field at point P. The loop is lying in x-y plane.

View SolutionThree identical wires are bent into semi-circular arcs to each of radius R. These arcs are connected with each other to form a closed mesh such that one of tham lies in x−y plane, one in y−z plane and the other in z−x plane as shown in. In the region of space, a uniform magnetic field of induction →B=B0(ˆi+ˆj) exists, whose magnitude increases at a constant rate dB/dt=α. Calculate the magnitude of emf induced in the mesh and mark the direction of flow of induced current in the mesh.

View SolutionA wire carrying current I has the shape as shown in adjoining figure. Linear parts of the wire are very long and parallel to X-axis while semicircular portion of radius R is lying in Y-Z plane. Magnetic field at point O is
View Solution

