A loop antenna of area 2.00 cm2 and resistance 5.21 μΩ. is perpendicular to a uniform magnetic field of magnitude 17.0 μT. The field magnitude drops to zero in 2.96 ms. How much thermal energy is produced in the loop by the change in field?
To solve the problem of how much thermal energy is produced in the loop by the change in the magnetic field, we will follow these steps:
Step 1: Identify the given values
- Area of the loop, A=2.00cm2=2.00×10−4m2
- Resistance of the loop, R=5.21μΩ=5.21×10−6Ω
- Initial magnetic field, B1=17.0μT=17.0×10−6T
- Final magnetic field, B2=0T
- Time duration for the change, t=2.96ms=2.96×10−3s
Step 2: Calculate the change in magnetic field
The change in magnetic field ΔB is given by:
ΔB=B2−B1=0−17.0×10−6=−17.0×10−6T
Step 3: Calculate the change in magnetic flux
The change in magnetic flux ΔΦ is given by:
ΔΦ=A⋅ΔB=(2.00×10−4m2)⋅(−17.0×10−6T)
Calculating this gives:
ΔΦ=−3.40×10−10Wb
Step 4: Calculate the induced EMF
Using Faraday's law of electromagnetic induction, the induced EMF ϵ is given by:
ϵ=−ΔΦΔt=−−3.40×10−10Wb2.96×10−3s
Calculating this gives:
ϵ=1.14865×10−7V
Step 5: Calculate the power
The power P dissipated in the resistor due to the induced EMF is given by:
P=ϵ2R
Substituting the values:
P=(1.14865×10−7)25.21×10−6
Calculating this gives:
P≈2.65×10−9W
Step 6: Calculate the thermal energy produced
The thermal energy Q produced in the loop is given by:
Q=P⋅t
Substituting the values:
Q=(2.65×10−9W)⋅(2.96×10−3s)
Calculating this gives:
Q≈7.85×10−12J
Final Answer
The thermal energy produced in the loop by the change in the magnetic field is approximately 7.85×10−12J.
---
- Area of the loop, A=2.00cm2=2.00×10−4m2
- Resistance of the loop, R=5.21μΩ=5.21×10−6Ω
- Initial magnetic field, B1=17.0μT=17.0×10−6T
- Final magnetic field, B2=0T
- Time duration for the change, t=2.96ms=2.96×10−3s
The change in magnetic field ΔB is given by:
ΔB=B2−B1=0−17.0×10−6=−17.0×10−6T
The change in magnetic flux ΔΦ is given by:
ΔΦ=A⋅ΔB=(2.00×10−4m2)⋅(−17.0×10−6T)
Calculating this gives:
ΔΦ=−3.40×10−10Wb
Using Faraday's law of electromagnetic induction, the induced EMF ϵ is given by:
ϵ=−ΔΦΔt=−−3.40×10−10Wb2.96×10−3s
Calculating this gives:
ϵ=1.14865×10−7V
The power P dissipated in the resistor due to the induced EMF is given by:
P=ϵ2R
Substituting the values:
P=(1.14865×10−7)25.21×10−6
Calculating this gives:
P≈2.65×10−9W
The thermal energy Q produced in the loop is given by:
Q=P⋅t
Substituting the values:
Q=(2.65×10−9W)⋅(2.96×10−3s)
Calculating this gives:
Q≈7.85×10−12J
The thermal energy produced in the loop by the change in the magnetic field is approximately 7.85×10−12J.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - PRACTICE QUESTIONS (Single Correct Choice Type)45videos
ELECTROMAGNETIC INDUCTION
- BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - PRACTICE QUESTIONS (More than One Correct Choice Type)13videos
ELECTROMAGNETIC INDUCTION
- BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - CHECKPOINTS9videos
ELECTROMAGNETIC INDUCTION
- BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - (PRACTICE QUESTIONS) Integer Type1videos
ELECTRIC POTENTIAL
- BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC OSCILLATIONS AND ALTERNATING CURRENT EXERCISE - Practice Questions (Integer)7videos
ELECTROMAGNETIC OSCILLATIONS AND ALTERNATING CURRENT
Similar Questions
The given loop is kept in a uniform magnetic field perpendicular to plane of loop. The field changes from 1000G to 500G in 5 seconds. the average induced emf in loop is
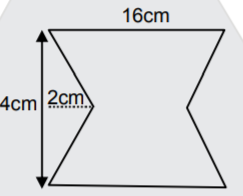-View SolutionA conducing circular loop having a radius of 5.0cm, is placed perpendicular to a magnetic field of 0.50 T. It is removed from the field in 0.50 s. Find the average emf produced In the loop during this time.
View Solution
Knowledge Check
- Question 1 - Select One
A circular loop of area 0.02m2 carrying a current of 10A, is held with its plane perpendicular to a magnetic field induction 0.2T. The torque acting on the loop is
A0.01 mB0.001 NmCzeroD0.8 Nm - Question 2 - Select One
A copper wire of length 50.0 cm and total resistance of 1.1×10−2Ω is formed into a circular loop and placed perpendicular to a uniform magnetic field that is increasing at the constant rate of 10.0 mT/s. At what rate is thermal energy generated in the loop?
A1.32×10−8WB2.36×10−4WC3.62×10−6WD4.23×10−5W - Question 3 - Select One
A square loop of side 22cm is converted into circular loop in 0.4s. A uniform magnetic field of 0.2Tdirected normal to the loop, then the induced in the loop is
A6.6×10−3VB6.6×10−5VC6.6×10−4VD6.6×10−8V
A square loop of side 20 cm and resistance 0.30 Ω is placed in a magnetic field of 0.4 T. The magnetic field is at an angle of 45∘ to the plane of loop. If the magnetic field is reduced to zero in 0.5 s, then find the induced emf and induced current in the loop in this time interval.
View SolutionIf 50.0 cm of copper wire (diameter= 3.00 mm) is formed into a circular loop and placed perpendicular to a uniform magnetic field that is increasing at the constant rate of 30.0 mT/s, at what rate is thermal energy generated in the loop?
View SolutionA metallic metre sitck moves with a velocity of 2 ms ^(-1) in a direction perpendicular to its length and perpendicular to a uniform magnetic field of magnitude 0.2 T. Find the emf indcued between the ends of the stick.
View SolutionA wire loop that encloses an area of 20cm2 has a resistance of 10Ω The loop is placed in a magnetic field of 2.4 T with its plane perpendicular to the field . The loop is suddenly removed from the field. How much charge flows past a given point in the wire ?
View SolutionA circular conducting loop of area 100cm2 and resistance 3Ω is placed in a magnetic field with its plane perpendicular to the field. If the field is spatially uniform but varies with time t (in second) as B(t)=1.5cosωt tesla, the peak value of the current in the loop is
View Solution