The graph gives the magnitude B(t) of a uniform magnetic field that exists throughout a conducting loop, with the direction of the field perpendicular to the plane of the loop. Rank the five regions of the graph according to the magnitude of the emf induced in the loop, greatest first.
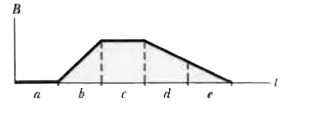
b, then d and e tie, and then a and c tie (zero)
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - PROBLEMS
67 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - PRACTICE QUESTIONS (Single Correct Choice Type)
45 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - PRACTICE QUESTIONS (Integer Type)
14 Videos
- ELECTRIC POTENTIALBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - (PRACTICE QUESTIONS) Integer Type
1 Videos
- ELECTROMAGNETIC OSCILLATIONS AND ALTERNATING CURRENT BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC OSCILLATIONS AND ALTERNATING CURRENT EXERCISE - Practice Questions (Integer)
7 Videos
Similar Questions
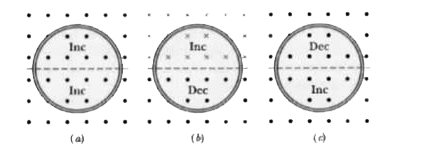
The figure shows three situations in which identical circular conducting loops are in uniform magnetic fields that are either increasing (Inc) or decreasing (Dec) in magnitude at identical rates. In each, the dashed line coincides with a diameter. Rank the situations according to the magnitude of the current induced in the loops, greatest first.
View SolutionThe given loop is kept in a uniform magnetic field perpendicular to plane of loop. The field changes from 1000G to 500G in 5 seconds. the average induced emf in loop is
-
View Solution
Knowledge Check
The graph gives the magnitude B (t) of a uniform magnetic field that exists throughout a conducting loop, perpendicular to the plane of the loop. Rank the five regions of the graph according to the magnitude of the emf induced in the loop, greatest first
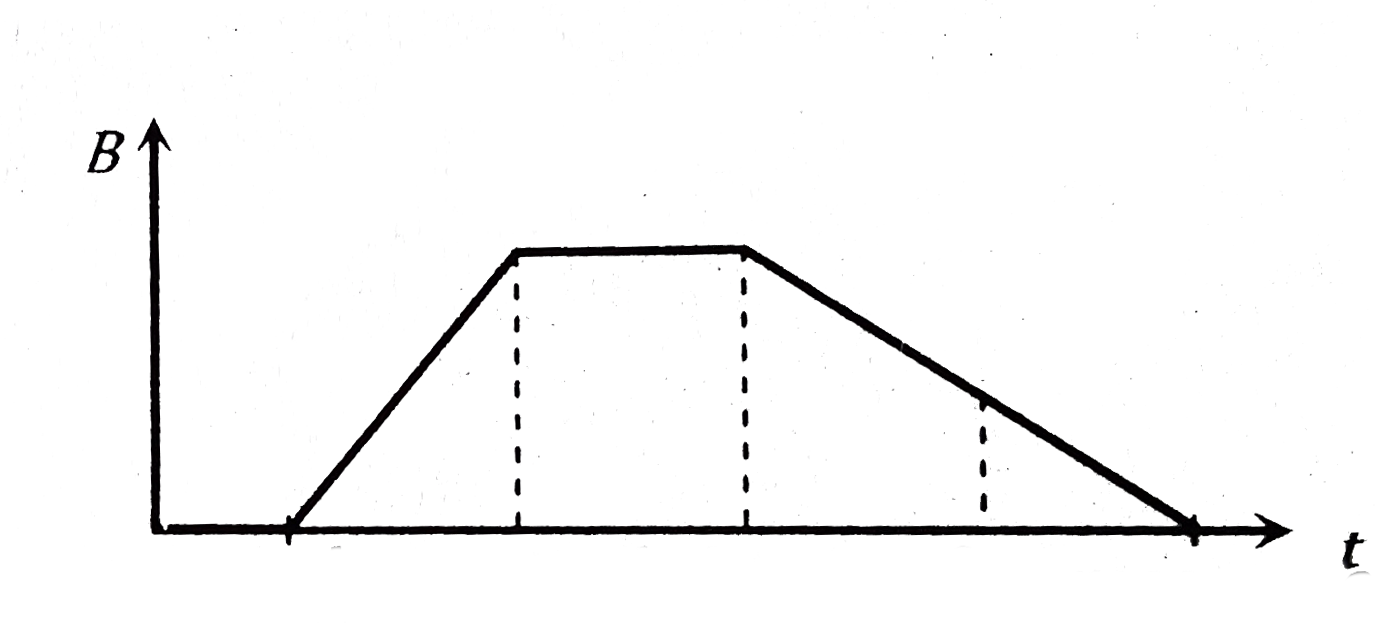Ab>(d=e)<(a=c)Bb<(d=e)>(a=c)Cb<d<e<c<aDb>(a=c)>(d=e)The graph gives the magnitude B(t) of a uniform magnetic field that exists throughout a conductig loop, perpendicular to the plane of the loop. Rank the five regions of the graph according to the magnitude fo the emf induced in the loop, greater first
Ab>(d=e)<(a=c)Bb>(d=e)>(a=c)Cb<d<e<c<aDb>(a=c)>(d=e)a conducting loop of radius R is precent in a uniform magnetic-field B perpendicular the plane of the ring. If radius R varies as a function of time 't', as R0+t. The e.m.f induced in the loop is
A2π(R0+t)B clockwiseBπ(R0+t)B clockwiseC2π(R0+t)B anticlockwiseDzero
Space is divided by the line AD into two regions. Region I is field free and the Region II has a unifrom magnetic field B direction into the plane of the paper. ACD is a simicircular conducting loop of radius r with center at O, hte plane of the loop being in the plane of the paper. The loop is now made to rotate with a constant angular velocity ω about an axis passing through O and the perpendicular to the plane of the paper. The effective resistance of the loop is R.
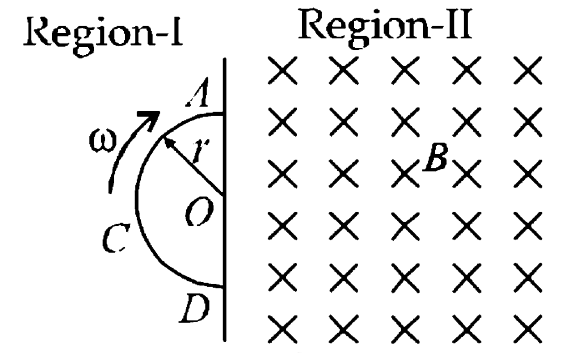
(i) obtain an expression for hte magnitude of the induced cureent in the loop.
(ii) Show the direction of the current when the loop is entering into the Rigion II.
Plot a graph between the induced e.m.f and the time of roation for two periods or rotation.
View SolutionA conducting loop of radius R is present in a uniform magnetic field B perpendicular to the plane of the ring. If radius R varies as a function of time t, as R=R0+t. The emf induced in the loop is
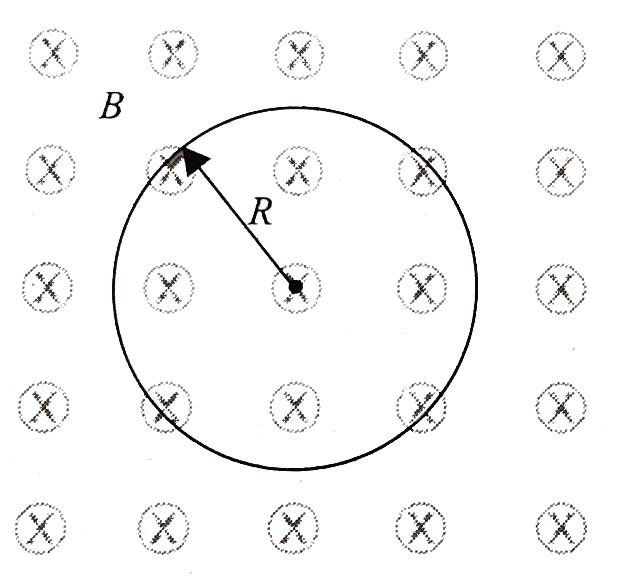
View SolutionA conducting loop of radius R is present in a uniform magnetic field B perpendicular to the plane of ring. If radius R varies as a function of time t as R=R0+t2. The emf induced in the loop is
View SolutionA conducting loop in the form of a circule is placed in a uniform magnetic field with its place perpendicular to the direction of the field. An e.m.f. will be induced in the loop if
View SolutionA conducting square loop is placed in a magnetic field B with its plane perpendicular to the field. Now the sides of the loop start shrinking at a constant rate α. the induced emf in the loop at an instant when its side is a is
View Solution