An infinite nonconducting sheet with a uniform surface charge density sets up parallel equipotential surfaces. Any pair of surfaces differing by 25.0 V are separated by 8.80 mm. (a) What is the magnitude of the surface charge density? (b) If an electron is released near the sheet, does it tend to move from higher to lower potential or vice versa ?
To solve the problem step by step, we will break it down into two parts as given in the question.
Part (a): Finding the Magnitude of the Surface Charge Density
1. Understanding the Electric Field and Potential Difference:
The electric field (E) between two equipotential surfaces is given by the formula:
E=−dVdx
where dV is the potential difference and dx is the distance between the surfaces.
2. Substituting the Given Values:
From the problem, we know:
- dV=25.0V
- dx=8.80mm=8.80×10−3m
Now, substituting these values into the formula for electric field:
E=25.0V8.80×10−3m
3. Calculating the Electric Field:
E=25.08.80×10−3≈2840.91N/C
4. Relating Electric Field to Surface Charge Density:
For an infinite non-conducting sheet, the electric field is related to the surface charge density (σ) by the formula:
E=σ2ϵ0
where ϵ0 (the permittivity of free space) is approximately 8.85×10−12C2/N m2.
5. Rearranging to Find Surface Charge Density:
Rearranging the formula gives:
σ=2Eϵ0
6. Substituting the Values:
σ=2×2840.91N/C×8.85×10−12C2/N m2
7. Calculating σ:
σ≈5.03×10−8C/m2
Part (b): Direction of Electron Movement
1. Understanding Electron Movement:
An electron is a negatively charged particle. In an electric field, it experiences a force in the direction opposite to the electric field.
2. Direction of Electric Field:
The electric field direction is from higher potential to lower potential. Therefore, the electron will move from lower potential to higher potential.
3. Conclusion:
Thus, if an electron is released near the sheet, it will tend to move from lower potential to higher potential.
Final Answers:
- (a) The magnitude of the surface charge density σ is approximately 5.03×10−8C/m2.
- (b) The electron tends to move from lower potential to higher potential.
The electric field (E) between two equipotential surfaces is given by the formula:
E=−dVdx
where dV is the potential difference and dx is the distance between the surfaces.
From the problem, we know:
- dV=25.0V
- dx=8.80mm=8.80×10−3m
E=25.0V8.80×10−3m
E=25.08.80×10−3≈2840.91N/C
For an infinite non-conducting sheet, the electric field is related to the surface charge density (σ) by the formula:
E=σ2ϵ0
where ϵ0 (the permittivity of free space) is approximately 8.85×10−12C2/N m2.
Rearranging the formula gives:
σ=2Eϵ0
σ=2×2840.91N/C×8.85×10−12C2/N m2
σ≈5.03×10−8C/m2
An electron is a negatively charged particle. In an electric field, it experiences a force in the direction opposite to the electric field.
The electric field direction is from higher potential to lower potential. Therefore, the electron will move from lower potential to higher potential.
Thus, if an electron is released near the sheet, it will tend to move from lower potential to higher potential.
- (a) The magnitude of the surface charge density σ is approximately 5.03×10−8C/m2.
- (b) The electron tends to move from lower potential to higher potential.
Topper's Solved these Questions
- ELECTRIC POTENTIALBook:RESNICK AND HALLIDAYChapter:ELECTRIC POTENTIALExercise:(PRACTICE QUESTIONS) Single Correct Choice Type
Explore 21 Videos
- ELECTRIC POTENTIALBook:RESNICK AND HALLIDAYChapter:ELECTRIC POTENTIALExercise:(PRACTICE QUESTIONS) More than One Correct Choice Type
Explore 8 Videos
- ELECTRIC POTENTIALBook:RESNICK AND HALLIDAYChapter:ELECTRIC POTENTIALExercise:CHECKPOINT
Explore 6 Videos
- ELECTRIC CHARGES AND FIELDSBook:RESNICK AND HALLIDAYChapter:ELECTRIC CHARGES AND FIELDSExercise:Practice Questions (Integer Type )
Explore 3 Videos
- ELECTROMAGNETIC INDUCTIONBook:RESNICK AND HALLIDAYChapter:ELECTROMAGNETIC INDUCTIONExercise:PRACTICE QUESTIONS (Integer Type)
Explore 14 Videos
Similar Questions
An infinite nonconducting sheet has a surface charge density of σ=0.10μC/m2 on one side. How far apart are equipotential surfaces whose potentials differ by 50 V?
View SolutionAn infinite conducting sheet has surface charge density σ. The distance between two points is r. The potential difference (VA−VB) between these point is
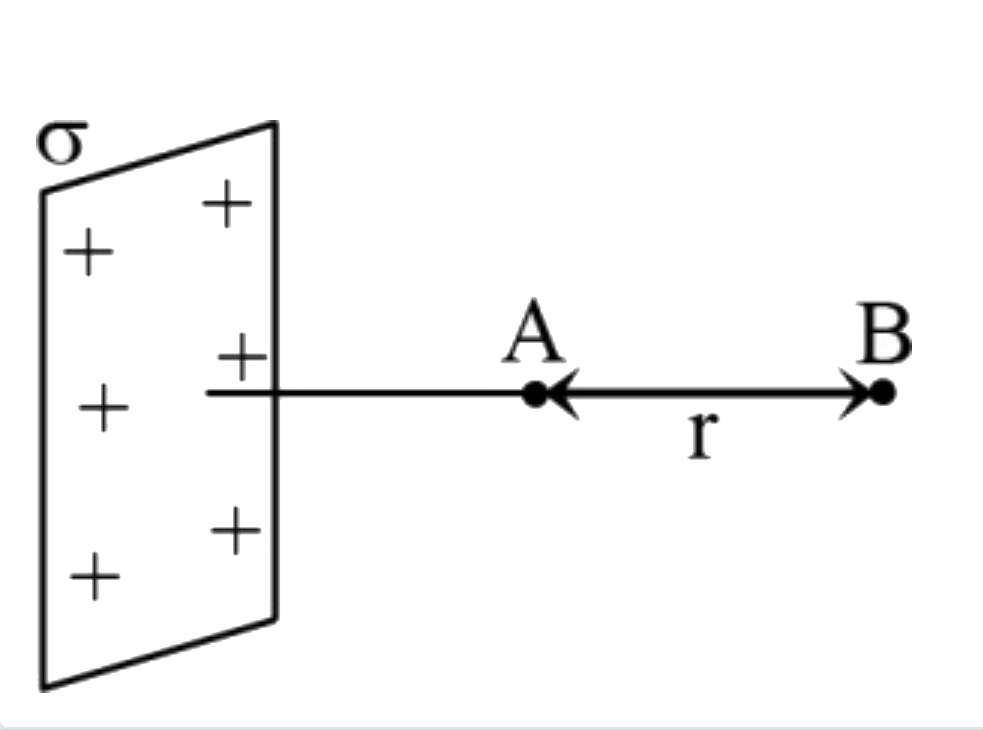
View Solution
Knowledge Check
An infinite sheet of charge has surface charge density σ . The separation between two equipotential surfaces, whose potential differ by V is:
AσV2∈0B2∈0VσC∈0VσD2σ∈0VAn infinite sheet of charge has a surfaces charge density of 10−7Cm2. The separation between two equipotential surfce whose potentials differ by 5V is
A0.64cmB0.88mmC0.32cmD5×10−7m
Electric field due to an infinite non-conducting sheet of surface charge density σ, at a distance r from it is
View SolutionTwo infinite non-conducting sheets each with uniform surface charge density sigma are kept in such a way that the angle between them is 30^(@). The electric field in the region I shown between them is
View SolutionAn infinite changed sheet has 10−7Cm−2 surface density of change .How far apart are the equipotential surface differing by 5 voits ?
[Hint: Elwctri intensity =rate of fall of potential .]
View SolutionA charged, conducting sphere of radius 5.5 cm sets up a potential of 75 V at a radial distance of 2.2 m (with V = 0 set at infinity). (a) What is the potential on the sphere's surface? (b) What is the surface charge density ?
View SolutionAn infinite plane sheet of charge density 10−8Cm−2 is held in air. In this situation how far apart are two equipotenitial surfaces, whose p.d is 5 V ?
View SolutionAn infinite thin non - conducting sheet has uniform surface charge density σ. Find the potential difference VA−VB between points A and B as shown in the figure. The line AB makes an angle of 37∘ with the normal to the sheet. (sin37∘=35)
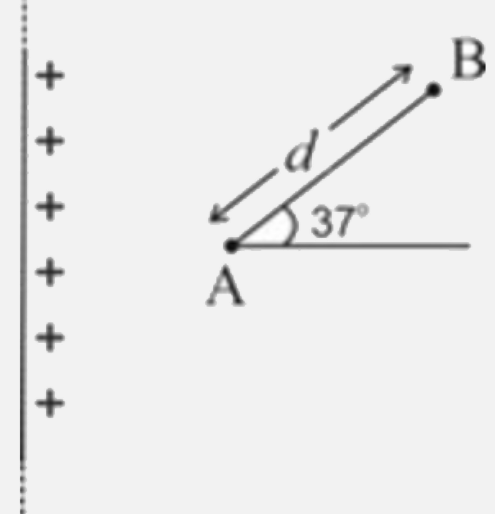
View Solution

