When a negative charge moves in a direction opposite to the direction of an electric field,
The field does work on the charge
The charge does work on the field
The charge gains potential energy
The charge loses potential energy
The correct Answer is:A, D
To solve the question regarding the movement of a negative charge in an electric field, we can break it down into a series of logical steps:
1. Understanding the Electric Field:
- An electric field (E) is defined as the region around a charged object where other charges experience a force. The direction of the electric field is from positive to negative charges.
2. Identifying the Charge and Its Movement:
- In this scenario, we have a negative charge (let's denote it as -Q) moving in a direction opposite to the electric field. If the electric field is directed to the right, the negative charge is moving to the left.
3. Applying Coulomb's Law:
- According to Coulomb's law, the force (F) experienced by a charge in an electric field is given by F=Q⋅E. For a negative charge, the force will be F=−Q⋅E. This indicates that the force on the negative charge will be in the opposite direction to the electric field.
4. Analyzing the Work Done:
- Work (W) done by a force is calculated using the formula W=F⋅d⋅cos(θ), where d is the displacement and θ is the angle between the force and displacement vectors.
- Since the force on the negative charge is in the opposite direction to the electric field, and the charge is moving in the opposite direction to the electric field, the work done by the electric field on the charge is positive.
5. Potential Energy Consideration:
- The potential energy (U) of a charge in an electric field is given by U=−Q⋅V, where V is the electric potential.
- As the negative charge moves against the electric field (from lower potential to higher potential), its potential energy increases. Therefore, the charge gains potential energy.
6. Conclusion:
- Based on the analysis, we conclude that:
- The electric field does work on the charge (Option A is correct).
- The charge gains potential energy (Option D is correct).
- Therefore, the correct options are A and D.
- An electric field (E) is defined as the region around a charged object where other charges experience a force. The direction of the electric field is from positive to negative charges.
- In this scenario, we have a negative charge (let's denote it as -Q) moving in a direction opposite to the electric field. If the electric field is directed to the right, the negative charge is moving to the left.
- According to Coulomb's law, the force (F) experienced by a charge in an electric field is given by F=Q⋅E. For a negative charge, the force will be F=−Q⋅E. This indicates that the force on the negative charge will be in the opposite direction to the electric field.
- Work (W) done by a force is calculated using the formula W=F⋅d⋅cos(θ), where d is the displacement and θ is the angle between the force and displacement vectors.
- Since the force on the negative charge is in the opposite direction to the electric field, and the charge is moving in the opposite direction to the electric field, the work done by the electric field on the charge is positive.
- The potential energy (U) of a charge in an electric field is given by U=−Q⋅V, where V is the electric potential.
- As the negative charge moves against the electric field (from lower potential to higher potential), its potential energy increases. Therefore, the charge gains potential energy.
- Based on the analysis, we conclude that:
- The electric field does work on the charge (Option A is correct).
- The charge gains potential energy (Option D is correct).
- Therefore, the correct options are A and D.
Topper's Solved these Questions
- ELECTRIC POTENTIALBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - (PRACTICE QUESTIONS) Linked Comprehension
2 Videos
- ELECTRIC POTENTIALBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - (PRACTICE QUESTIONS) Matrix-Match
4 Videos
- ELECTRIC POTENTIALBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - (PRACTICE QUESTIONS) Single Correct Choice Type
21 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Practice Questions (Integer Type )
3 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - PRACTICE QUESTIONS (Integer Type)
14 Videos
Similar Questions
Show that drift velocity is in a direction opposite to the drirection of electric field applied across two ends of the conductor.
View SolutionThe given diagram shows two infinite line of charges having equal (in magnitude) linear charge density but with opposite sign. The direction of electric field at any point on x-axis for (x>0) is given by the unit vector
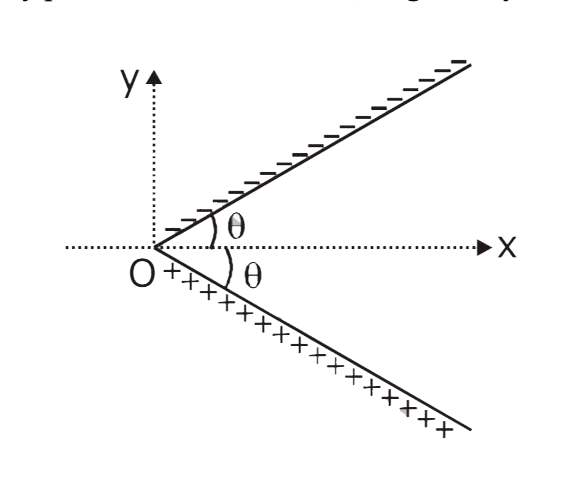
View Solution
Knowledge Check
A negative charge is moved by an external agent in the direction of electric field. Then
.APotential energy of the charge increases.BPotential energy of the charge decreases.CPositive work is done by the electric fieldDnegative work is done by the electric fieldA spinning ball is moving in a direction opposite to the direction of the wind. The ball moves in a curved path as
Athe pressure at the top and the bottom of the ball are equal.Bthe pressure at the top > thre pressure at the bottomCthe pressure at the top < the pressure at the bottomDthere is no relation between the pressures.An electron having a charge c moves with a velocity v in X - direction . An electric field acts on it in Y - direction ? The force on the electron acts in
Apositive direction of Y - axisBnegative direction of Y - axisCpositive direction of Z - axisDnegative direction of Z - axis
What is the convention for direction of an electric field?'
View SolutionWill the potential energy of a negative charge increases or decreases when it is moved in the direction of electric field? Will its final position be at higher potential or lower potential?
View SolutionFor the given figure the direction of electric field at A will be
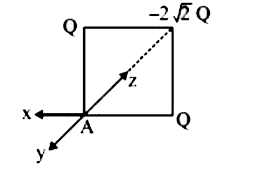
View SolutionAssertion: Electric field intensity at a point due to a positive charge is always opposite in direction to electric field intensity due to negative charge, and it is independent to locațions of charges.
Reason: The direction of electric field due to a point charge is away from the positive charge and towards the negative charge along the line joining the point charge and location where the electric field is to be calculated.
View SolutionThe given figure represents a portion of a wire in a circuit. A current is flowing in the wire in the direcnon shown. Under the convention that is positive charge that flows, the electric field point field in the direction of the charge rent. There will be some charge
accumulation at the bend to change the direction of the electric field. What is the direction of the electric field due to charges at the bend?
View Solution