The electric field in a region of space has the components Ey=Ez=0andEx=(4.00N/C)x2. Point A is on the y axis at y = 3.00 m, and point B is on the x axis at x = 4.00 m. What is the potential difference VB−VA ?
To find the potential difference VB−VA between points A and B in the given electric field, we can follow these steps:
Step 1: Understand the Electric Field
The electric field components are given as:
- Ey=0
- Ez=0
- Ex=4.00N/C⋅x2
This indicates that the electric field only has a component in the x-direction, and it varies with x.
Step 2: Identify the Points
Point A is located on the y-axis at y=3.00m (so its coordinates are (0,3,0)), and point B is on the x-axis at x=4.00m (so its coordinates are (4,0,0)).
Step 3: Write the Formula for Potential Difference
The potential difference between two points in an electric field can be calculated using the formula:
VB−VA=−∫BA→E⋅d→l
Here, d→l is the differential path element along the path from A to B.
Step 4: Determine the Path of Integration
Since point A is at (0,3,0) and point B is at (4,0,0), we can move from A to B along the x-axis. The path can be taken as moving from x=0 to x=4 while keeping y=3 constant.
Step 5: Set Up the Integral
Since Ey=0 and Ez=0, the only component contributing to the potential difference is Ex:
VB−VA=−∫40Exdx
Substituting Ex=4.00N/C⋅x2:
VB−VA=−∫40(4.00x2)dx
Step 6: Perform the Integration
Now we integrate:
VB−VA=−4.00∫40x2dx
Calculating the integral:
∫x2dx=x33
Thus,
VB−VA=−4.00(x33)40=−4.00(433−033)=−4.00(643)
Calculating this gives:
VB−VA=−2563V
Step 7: Final Result
Calculating the numerical value:
VB−VA≈−85.33V
Summary
The potential difference VB−VA is approximately −85.33V.
---
The electric field components are given as:
- Ey=0
- Ez=0
- Ex=4.00N/C⋅x2
Point A is located on the y-axis at y=3.00m (so its coordinates are (0,3,0)), and point B is on the x-axis at x=4.00m (so its coordinates are (4,0,0)).
The potential difference between two points in an electric field can be calculated using the formula:
VB−VA=−∫BA→E⋅d→l
Here, d→l is the differential path element along the path from A to B.
Since point A is at (0,3,0) and point B is at (4,0,0), we can move from A to B along the x-axis. The path can be taken as moving from x=0 to x=4 while keeping y=3 constant.
Since Ey=0 and Ez=0, the only component contributing to the potential difference is Ex:
VB−VA=−∫40Exdx
Substituting Ex=4.00N/C⋅x2:
VB−VA=−∫40(4.00x2)dx
Now we integrate:
VB−VA=−4.00∫40x2dx
Calculating the integral:
∫x2dx=x33
Thus,
VB−VA=−4.00(x33)40=−4.00(433−033)=−4.00(643)
Calculating this gives:
VB−VA=−2563V
Calculating the numerical value:
VB−VA≈−85.33V
The potential difference VB−VA is approximately −85.33V.
Topper's Solved these Questions
- ELECTRIC POTENTIALBook:RESNICK AND HALLIDAYChapter:ELECTRIC POTENTIALExercise:(PRACTICE QUESTIONS) Single Correct Choice Type
Explore 21 Videos
- ELECTRIC POTENTIALBook:RESNICK AND HALLIDAYChapter:ELECTRIC POTENTIALExercise:(PRACTICE QUESTIONS) More than One Correct Choice Type
Explore 8 Videos
- ELECTRIC POTENTIALBook:RESNICK AND HALLIDAYChapter:ELECTRIC POTENTIALExercise:CHECKPOINT
Explore 6 Videos
- ELECTRIC CHARGES AND FIELDSBook:RESNICK AND HALLIDAYChapter:ELECTRIC CHARGES AND FIELDSExercise:Practice Questions (Integer Type )
Explore 3 Videos
- ELECTROMAGNETIC INDUCTIONBook:RESNICK AND HALLIDAYChapter:ELECTROMAGNETIC INDUCTIONExercise:PRACTICE QUESTIONS (Integer Type)
Explore 14 Videos
Similar Questions
The electric field in a region of space is given as ¯¯¯E=(5xˆi−2ˆj) .Potential at point x =1 y=1 is V1 and potential at point x =2 y=3 is V2 .ThenV1−V2 is equal to
View SolutionThe electric field in a region of space is given as ¯¯¯E=(5xˆi−2ˆj) .Potential at point x=1 y=1 is V1 and potential at point (x=2 y=3) is V2 .Then V1−V2 is equal to
View Solution
Knowledge Check
In a certain region, electric field E exists along the x - axis which is uniform. Given B=2√3m and BC=4m. Points A, B, and C are in xy plane.
 .
.
find the potential difference VC−VB between the points CandB.A2 EB3 EC−ED−2EIn a certain region, electric field E exists along the x - axis which is uniform. Given B=2√3m and BC=4m. Points A, B, and C are in xy plane.
 .
.
Find the potential difference VA−VB between the points AandB.A3 EB4 ECED2 EA graph of the x-component of the electric field as a function of x in a region of space is shown in figure. The y−andz−compo≠nts of the electric field are zero in this region. If the electric potential is 10 V at the origin, then the potential at x = 2.0 m is
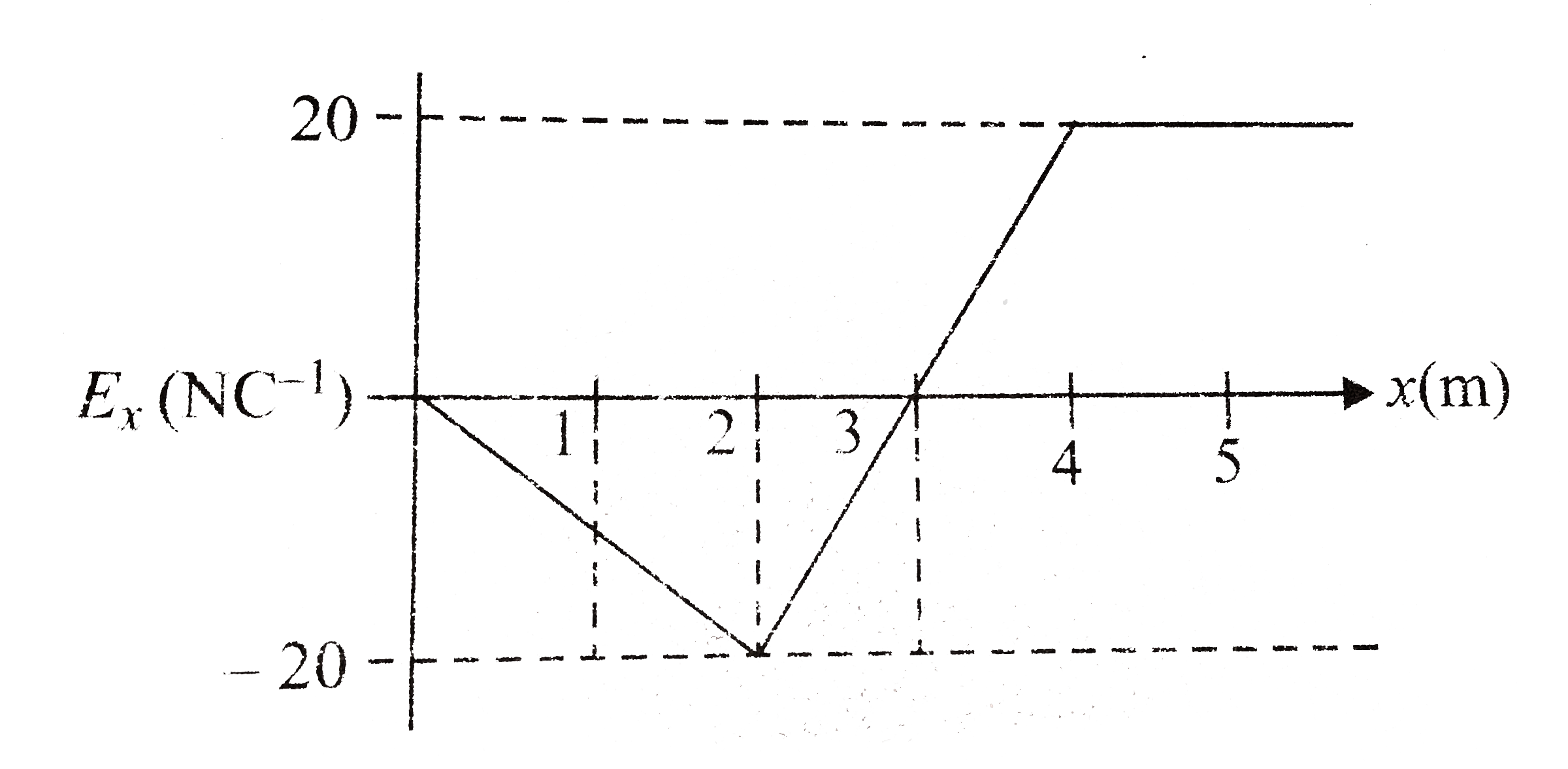 A10VB40VC−10VD30V
A10VB40VC−10VD30V
A plane electromagnetic wave traveling in the positive direction of an x axis in vacuum has components Ex=Ey=0 and Ez=(4.0V/m)cos[(π×1015s−1)(t−x/c)] . (a) What is the amplitude of the magnetic field component ? (b) Parallel to Which axis does the magnetic field oscillate ? (c ) When the electric field component field oscillate ? (c ) When teh electric field component is in the the positive direction of the z axis at a certain point P what is the direction of the magnetic field component there ? (d) In what direction is the wave moving ?
View SolutionElectric potential in a region of space is given by V=(x2+y2+z2)V. What will be electric field intensity at a point P(-1m, 2m, -3m)?
View SolutionA positively charged particle, having charge q, is accelerated by a potential difference V. This particle moving along the x-axis enters a region where an electric field E exists. The direction of the electric field is along positive y-axis. The electric field exists in the region bounded by the lines x=0andx=a. Beyond the line x=a (i.e., in the region x>a), there exists a magnetic field of strength B, directed along the positive y-axis. Find

a. at which point does the particle meet the line x=a.
b. the pitch of the helix formed after the particle enters the region x≥a. (Mass of the particle is m.)
View SolutionThe electric potential in aregion of space is given by V=(5x−7x2y+8y2+16yz−4z) volt. The y-component of the electric field at the point (2,4,−3) is
View SolutionIf the potentail in the region of space around the point (−1m,2m,3m) is given by V=(10x2+5y2−3z2), calculate the three components of electric field at this point.
View Solution

