An automobile can be considered to be mounted on four identical springs as far as vertical oscillations are concerned. The springs of a certain car are adjusted so that the oscillations have a frequency of 3.00Hz. (a) What is the spring constant of each spring if the mass of the car is 2110kg and the mass is evenly distributed over the springs? (b) What will be the oscillation frequency if five passengers, averaging 85.0kg each, ride in the car with an even distribution of mass?
To solve the problem, we will break it down into two parts as given in the question.
Part (a): Finding the Spring Constant
1. Identify the Given Data:
- Frequency of oscillation, f=3.00Hz
- Mass of the car, m=2110kg
- Number of springs, n=4
2. Use the Formula for Angular Frequency:
The angular frequency ω is related to the frequency f by the formula:
ω=2πf
Substituting the given frequency:
ω=2π×3.00=6πrad/s
3. Relate Angular Frequency to Spring Constant:
The angular frequency is also related to the spring constant k and mass m by the formula:
ω=√keqm
Where keq is the equivalent spring constant for the four springs in parallel. Since all springs are identical:
keq=4k
4. Substituting into the Angular Frequency Formula:
We can substitute keq into the angular frequency formula:
6π=√4k2110
5. Square Both Sides:
(6π)2=4k2110
6. Solve for k:
36π2=4k2110
k=36π2×21104
k≈36×9.87×21104≈1.87×105N/m
Part (b): Finding the New Oscillation Frequency with Passengers
1. Calculate the Total Mass with Passengers:
- Average mass of each passenger = 85.0 kg
- Total mass of 5 passengers = 5×85=425kg
- New total mass m′=2110+425=2535kg
2. Use the Spring Constant from Part (a):
We already calculated k in part (a):
k≈1.87×105N/m
3. Calculate New Angular Frequency:
Using the same formula for angular frequency:
ω′=√keqm′
ω′=√4k2535
4. Substituting the Value of k:
ω′=√4×1.87×1052535
5. Calculate the New Frequency:
f′=ω′2π
6. Final Calculation:
ω′≈√7480002535≈17.17rad/s
f′≈17.172π≈2.73Hz
Summary of Answers:
- (a) The spring constant of each spring is approximately 1.87×105N/m.
- (b) The new oscillation frequency with passengers is approximately 2.73Hz.
- Frequency of oscillation, f=3.00Hz
- Mass of the car, m=2110kg
- Number of springs, n=4
The angular frequency ω is related to the frequency f by the formula:
ω=2πf
Substituting the given frequency:
ω=2π×3.00=6πrad/s
The angular frequency is also related to the spring constant k and mass m by the formula:
ω=√keqm
Where keq is the equivalent spring constant for the four springs in parallel. Since all springs are identical:
keq=4k
We can substitute keq into the angular frequency formula:
6π=√4k2110
(6π)2=4k2110
36π2=4k2110
k=36π2×21104
k≈36×9.87×21104≈1.87×105N/m
- Average mass of each passenger = 85.0 kg
- Total mass of 5 passengers = 5×85=425kg
- New total mass m′=2110+425=2535kg
We already calculated k in part (a):
k≈1.87×105N/m
Using the same formula for angular frequency:
ω′=√keqm′
ω′=√4k2535
ω′=√4×1.87×1052535
f′=ω′2π
ω′≈√7480002535≈17.17rad/s
f′≈17.172π≈2.73Hz
- (a) The spring constant of each spring is approximately 1.87×105N/m.
- (b) The new oscillation frequency with passengers is approximately 2.73Hz.
Topper's Solved these Questions
- OSCILLATIONSBook:RESNICK AND HALLIDAYChapter:OSCILLATIONSExercise:Practice Questions
Explore 57 Videos
- OSCILLATIONSBook:RESNICK AND HALLIDAYChapter:OSCILLATIONSExercise:Checkpoint
Explore 8 Videos
- MOTION IN TWO AND THREE DIMENSIONSBook:RESNICK AND HALLIDAYChapter:MOTION IN TWO AND THREE DIMENSIONSExercise:PRACTICE QUESTIONS (MATRIX-MATCH)
Explore 10 Videos
- PHOTONS AND MATTER WAVESBook:RESNICK AND HALLIDAYChapter:PHOTONS AND MATTER WAVESExercise:PRACTICE QUESTIONS(Integer Type)
Explore 4 Videos
Similar Questions
Find the time period of the oscillation of mass m in figure a,b,c what is the equivalent spring constant of the pair oif springs in each case?
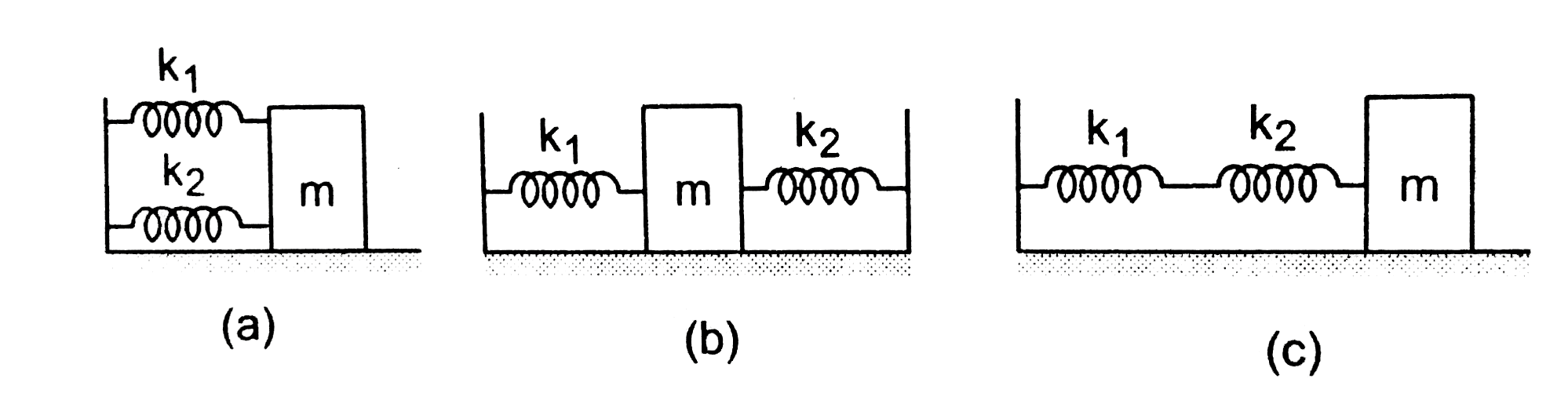
View SolutionTwo identical springs, each of spring factor k, may be connected in the following ways. Deduce the spring factor of the oscillation of the body in each case.
View Solution
Knowledge Check
A body of mass 20 g connected to a spring of spring constant k, executes simple harmonic motion with a frequency of (5/π) Hz. The value of spring constant is
A4Nm−1B3Nm−1C2Nm−1D5Nm−1The frequency of vertical oscillations of the three spring-mass system, shown in figure, is
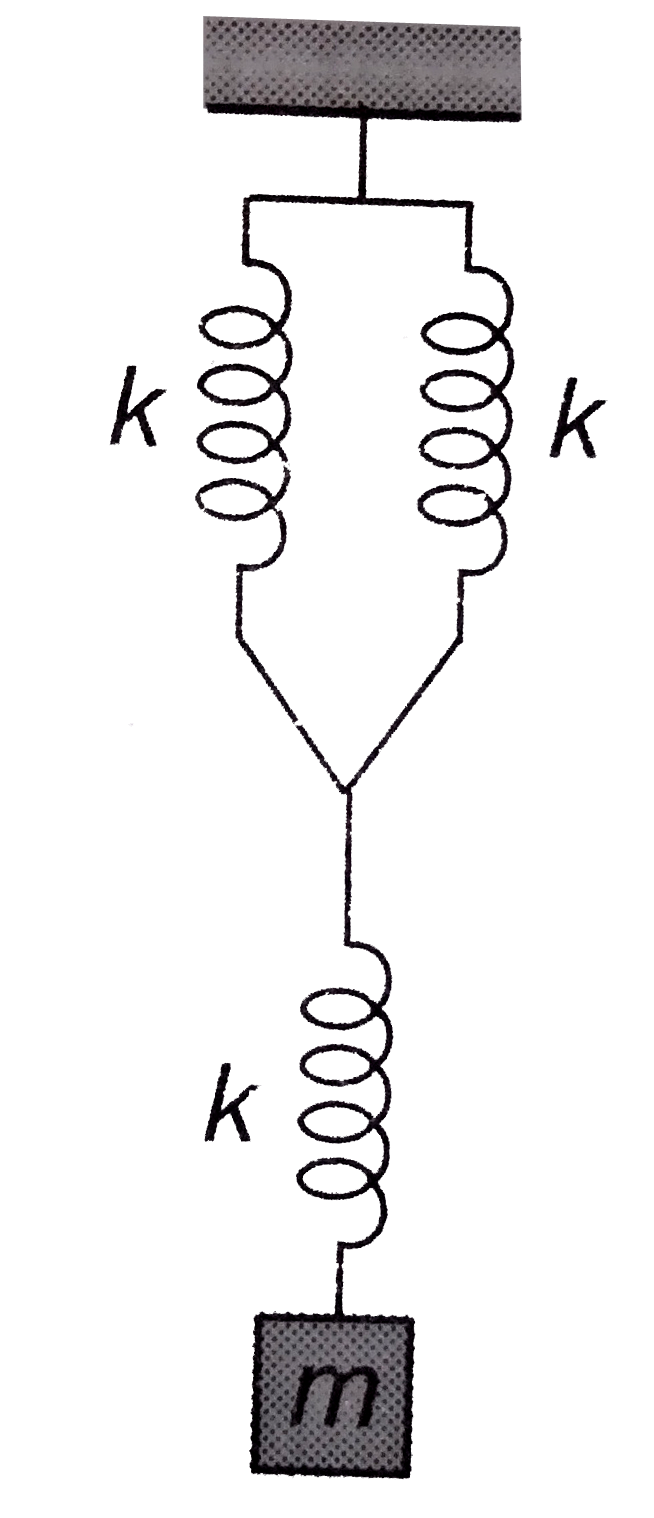 A12π√3k2mB12π√2k3mC12π√2kmD12π√k3m
A12π√3k2mB12π√2k3mC12π√2kmD12π√k3mThe frequency of oscillation of the springs shown in the figure will be
 A12π√KmB12π√(K1+K2)K1K2C12π√kmD12π√K1K2m(K1+K2)
A12π√KmB12π√(K1+K2)K1K2C12π√kmD12π√K1K2m(K1+K2)
Two identical springs S1andS2 are joined as shown in the figure. The oscillation frequency of the mass m is v. What will be the frequency of mass m, if one spring is removed ?

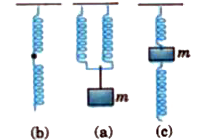
View SolutionTwo identical springs (springs constant K) are connected together in three different ways. In which case will the spring factor of the oscillation of the body be least ?
View SolutionA spring mass system oscillates in a car. If the car accelerates on a horizontal road, the frequency of oscillation will
View SolutionExplain the oscillations of a loaded spring and find the realtions for the time period and frequency in case of (i) horizontal spring (ii) vertical spring.
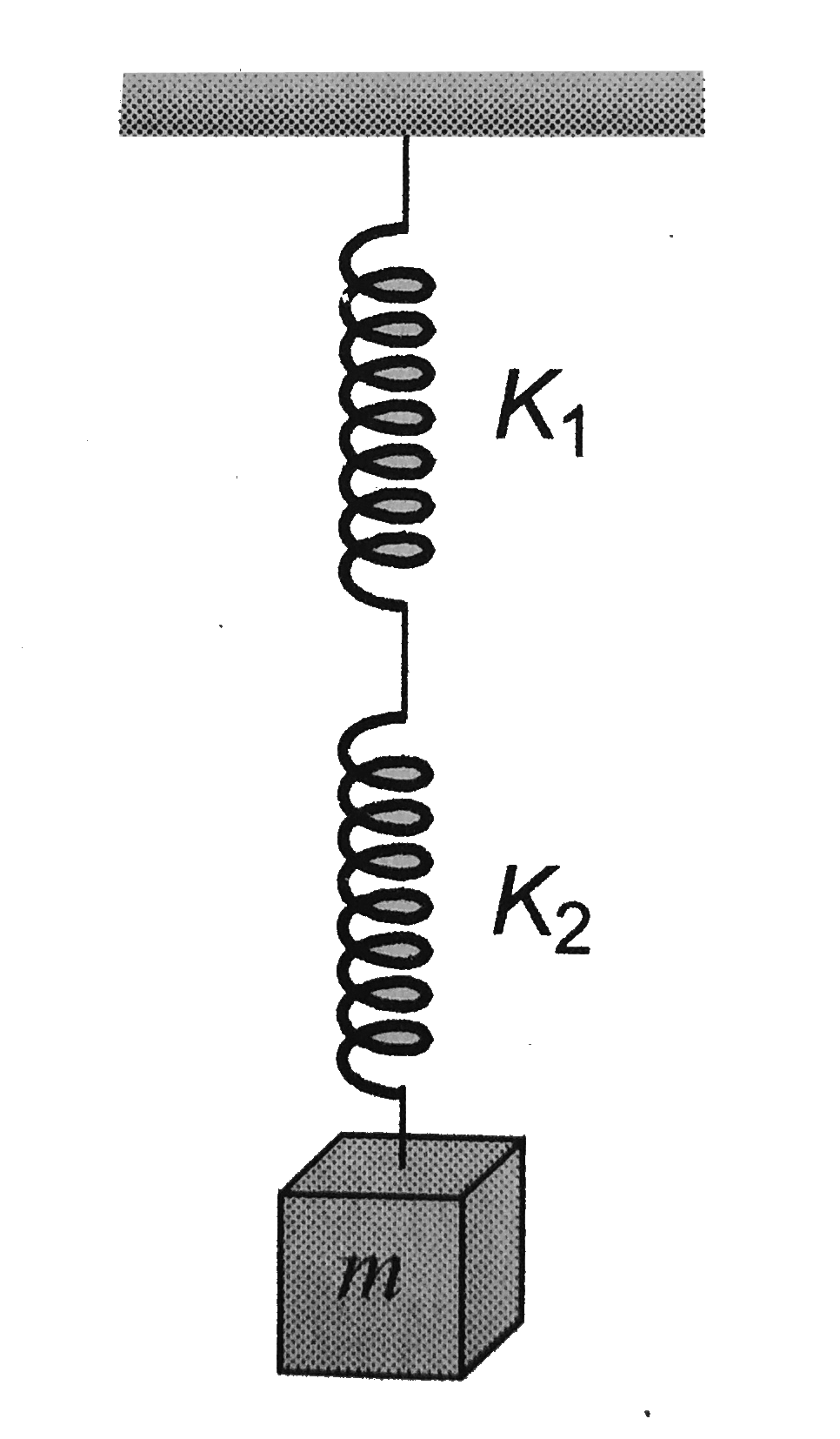
View SolutionThe frequency of oscillation of the spring shown in the figure will be
View Solution

