In Fig. 15.33, a stick of length L= 1.65 m oscillates as a physical pendulum. (a) What value of distance x between the stick's center of mass and its pivot point O gives the least period? (b) What is that least period?
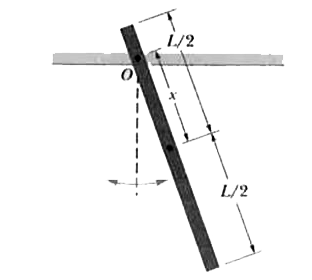
x= 0.48m, (b) T= 2.0s
Topper's Solved these Questions
- OSCILLATIONSBook:RESNICK AND HALLIDAYChapter:OSCILLATIONSExercise:Practice Questions
Explore 57 Videos
- OSCILLATIONSBook:RESNICK AND HALLIDAYChapter:OSCILLATIONSExercise:Checkpoint
Explore 8 Videos
- MOTION IN TWO AND THREE DIMENSIONSBook:RESNICK AND HALLIDAYChapter:MOTION IN TWO AND THREE DIMENSIONSExercise:PRACTICE QUESTIONS (MATRIX-MATCH)
Explore 10 Videos
- PHOTONS AND MATTER WAVESBook:RESNICK AND HALLIDAYChapter:PHOTONS AND MATTER WAVESExercise:PRACTICE QUESTIONS(Integer Type)
Explore 4 Videos
Similar Questions
In Fig 15.19a, a meter stick swings about a pivot point at one end, at distance h from the stick's center of mass.
What is the period of oscillation T?
View SolutionIn Fig 15.19a, a meter stick swings about a pivot point at one end, at distance h from the stick's center of mass.
What is the distance L0 between the pivot point O of the stick and the center of oscillation of the stick?
View Solution
Knowledge Check
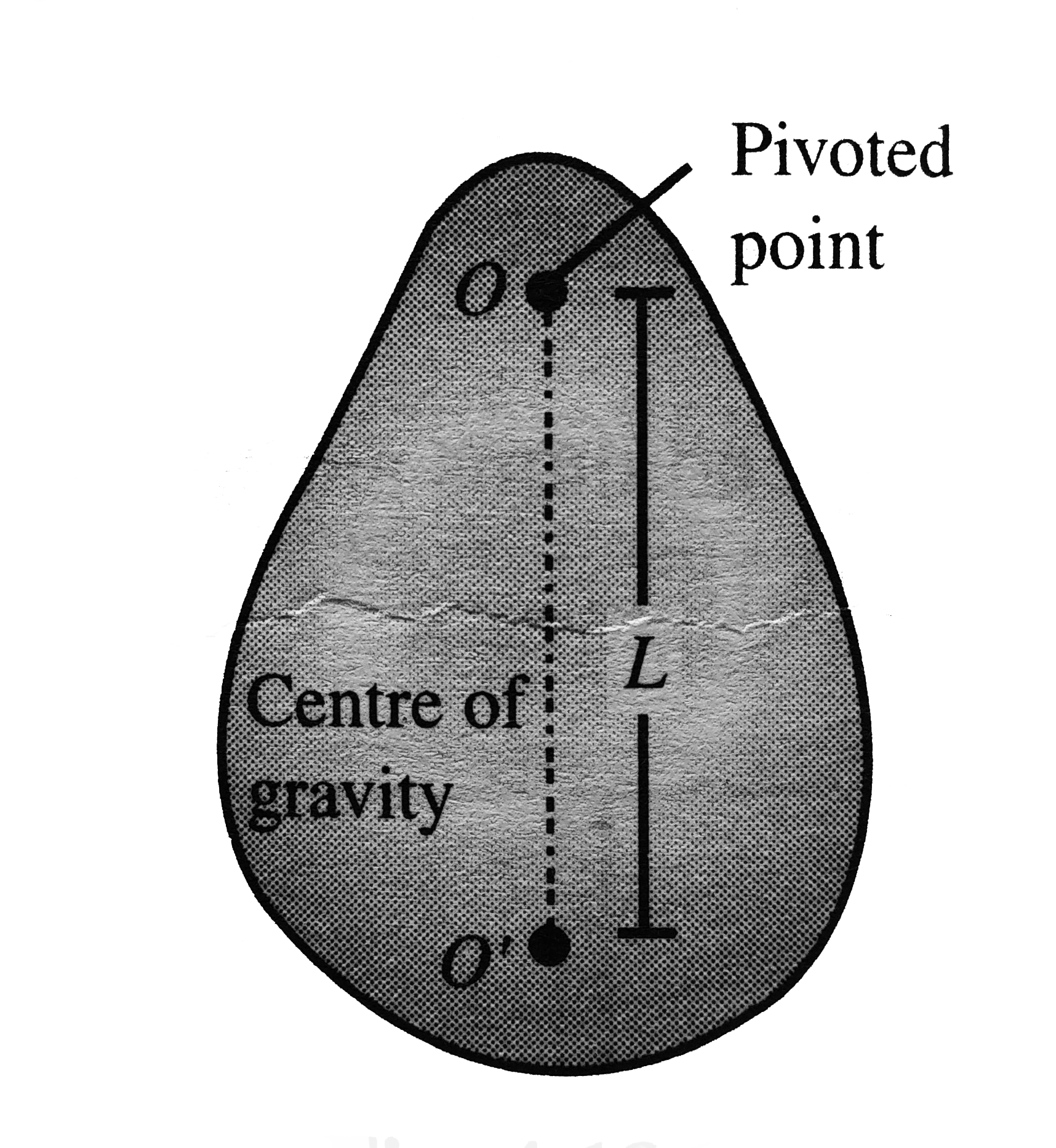
In physical pendulum, the time period for small oscillation is given by T=2π√IMgd where I is the moment of inertial of the body about an axis passing through a pivoted point O and perpendicular to the plane of oscillation and d is the separation point between centre of gravity and the pivoted point. In the physical pendulum a speacial point exists where if we concentrate the entire mass of body, the resulting simple pendulum (w.r.t. pivot point O) will have the same time period as that of physical pendulum This point is termed centre of oscillation.
T=2π√IMgd=2π√Lg Moreover, this point possesses two other important remarkable properties:
Property I: Time period of physical pendulum about the centre of oscillation (if it would be pivoted) is same as in the original case.
Property II: If an impulse is applied at the centre of oscillatioin in the plane of oscillation, the effect of this impulse at pivoted point is zero. Because of this property, this point is also known as the centre of percussion. From the given information answer the following question:
Q. A uniform rod of mass M and length L is pivoted about point O as shown in Figgt It is slightly rotated from its mean position so that it performs angular simple harmonic motion. For this physical pendulum, determine the time period oscillation.A2π√LgBπ√7L3gC2π√2l3gDnone of theseIn physical pendulum, the time period for small oscillation is given by T=2π√IMgd where I is the moment of inertial of the body about an axis passing through a pivoted point O and perpendicular to the plane of oscillation and d is the separation point between centre of gravity and the pivoted point. In the physical pendulum a speacial point exists where if we concentrate the entire mass of body, the resulting simple pendulum (w.r.t. pivot point O) will have the same time period as that of physical pendulum This point is termed centre of oscillation.
T=2π√IMgd=2π√Lg Moreover, this point possesses two other important remarkable properties:
Property I: Time period of physical pendulum about the centre of oscillation (if it would be pivoted) is same as in the original case.
Property II: If an impulse is applied at the centre of oscillatioin in the plane of oscillation, the effect of this impulse at pivoted point is zero. Because of this property, this point is also known as the centre of percussion. From the given information answer the following question:
Q. If an impulse J is applied at the centre of oscillation in the plane of oscillation, then angular velocity of the rod will be .
 A4JMLB2JMLC3J2MLDJML
A4JMLB2JMLC3J2MLDJMLIn physical pendulum, the time period for small oscillation is given by T=2π√IMgd where I is the moment of inertial of the body about an axis passing through a pivoted point O and perpendicular to the plane of oscillation and d is the separation point between centre of gravity and the pivoted point. In the physical pendulum a speacial point exists where if we concentrate the entire mass of body, the resulting simple pendulum (w.r.t. pivot point O) will have the same time period as that of physical pendulum This point is termed centre of oscillation.
T=2π√IMgd=2π√Lg Moreover, this point possesses two other important remarkable properties:
Property I: Time period of physical pendulum about the centre of oscillation (if it would be pivoted) is same as in the original case.
Property II: If an impulse is applied at the centre of oscillatioin in the plane of oscillation, the effect of this impulse at pivoted point is zero. Because of this property, this point is also known as the centre of percussion. From the given information answer the following question:
Q. For the above question, locate the centre of oscillation.
 AL4 from O (down)BL4 from O (up)C2L3 from O (down)D7L12 from O (down)
AL4 from O (down)BL4 from O (up)C2L3 from O (down)D7L12 from O (down)
A uniform stick of length l is hinged so as to rotated about a harmonic axis perpendicular to the stick, at a distance from the center . Find the value of x, for which the time period is minimum.
View SolutionA pendulum is formed by pivoting a long thin rod about a point on the rod. In a series of experiments, the period is measured as a function of the distance x between the pivot point and the rod's center. (a) If the rod's length is L= 2.20 m and its mass is m= 22.1g, what is the minimum period? (b) If x is chosen to minimize the period and then L is increased does the period increase, decrease, or remain the same? (c ) If, instead, m is increased without L increasing does the period increase, decrease or remain the same?
View SolutionA meter stick of negligible mass can rotate about a vertical axis through a point at distant x from the point marked "0". A small block of mass 0.100 kg is glued at the mark of "0" and a small block of mass 0.500 kg is glued at the opposite end, at the mark of "1." The stick and blocks are to rotate with an angular speed of 5.00 rad/min. (a) For what choice of x is the associated rotational kinetic energy least and (b) what is that least erergy?
View SolutionA uniform stick of length l is mounted so as to rotate about a horizontal axis perpendicular to the stick and at a distance d from the centre of mass. The time period of small oscillation has a minimum value when d/l is
View SolutionThe time period of a physical pendulum about some pivot point is T. When we take another pivot point, opposite of the first one such that the centre of mass of the physical pendulum lies on the line joining these two pivot points, we obtain the same time period. If the two points are separated by a distance L, then the time period T is
View Solution

