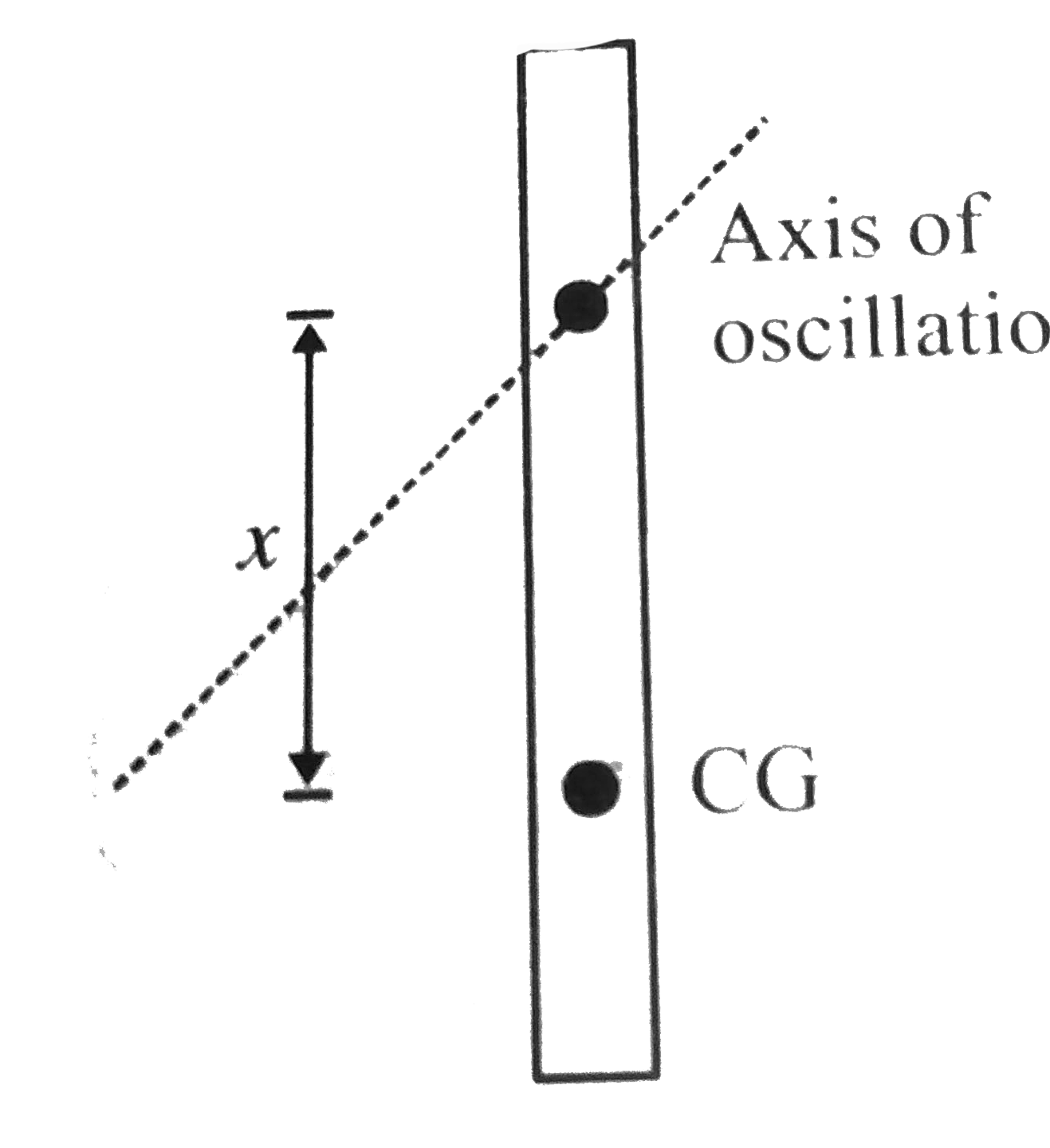
A uniform stick of length l is hinged so as to rotated about a harmoni

A uniform stick of length $l$ is mounted so as to rotate about a horizontal axis perpendicular to the stick and at a distance $d$ from the centre of mass. The time period of small oscillation has a minimum value when $d / l$ is
A $\frac{1}{\sqrt{2}}$
B $\frac{1}{\sqrt{12}}$
C $\frac{1}{\sqrt{3}}$
D $\frac{1}{\sqrt{6}}$
The moment of inertia of a thin rod of mass M and length L about an axis perpendicular to the rod at a distance L/4 from one end is
A $\frac{M L^{2}}{6}$
B $\frac{M L^{2}}{12}$
C $\frac{7 M L^{2}}{24}$
D $\frac{7 M L^{2}}{48}$
A uniform stick of length l and mass m lies on a smooth table. It rotates with angular velocity $ω$ about an axis perpendicular to the table and through one end of the stick. The angular momentum of the stick about the end is
A $m l^{2} ω$
B $\frac{m l^{2} ω}{3}$
C $\frac{m l^{2} ω}{12}$
D $\frac{m l^{2} ω}{6}$

A uniform stick of length l is hinged so as to rotated about a harmonic axis perpendicular to the stick, at a distance from the center . Find the value of x, for which the time period is minimum.