A simple pendulum of length l swings from a small angle θ . Its swinging is constrained by the smooth inclined planes OP and PC. Assuming elastic collision of the bob with the plane PC, find
a. angular amplitude for the motion of the bob in the left hand side of its mean position.
b. time period for a complete cycle of motion of the bob.

a. Let us assume that the bob swings a maximum a maximum angle β in the left hand side of the mean position in the absence of the position PC of the wall.
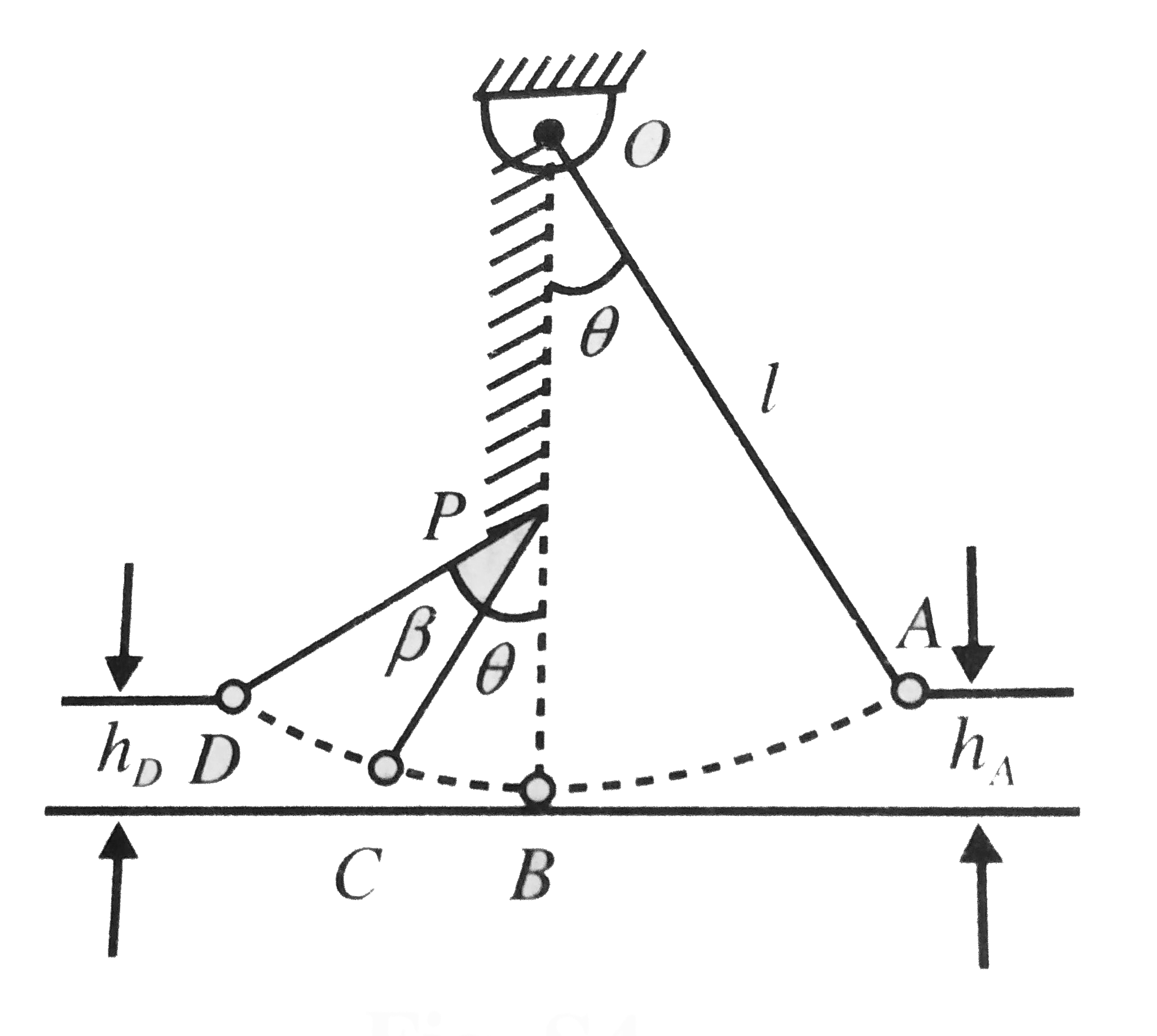
Conserving energy at A and D, we have
UA+KA=UD+KD
where UA=mghA.UB=mghB
and KA=KD=0
because the bob compes to rest at the exterme positions.
Then, we have hA=hD
Substituting hA=OA(1−cosθ)
and h0=PA(1−cosθ) we have
OA(1−cosθ)=PD(1−cosβ)
Substituting OA=l.PD=(l−d), we have
β=(√ll−h)θ
b. Since the bob from A to B
tAB=T4
where T=2π√lg
Then tAB=π2√lg
The time of miotion from B to C can be found by subsituting
t=tBC.θ=0
and θ=β√(l/(l−h))θ
in the equation θ=θ0sinωt.
where ω=√g/(l−h)
for the swinging position of the string from B to C. This gives
θ=√ll−hθsin√gl−htBC
Then, we have
tBC=√l−hgsin−1√l−hl
Finally, substituting tABandtBC in the expression of time . T=2(tAB+tBC) , we have
T=π√lg+√l−hlsin−1√l−hl
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICSChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Subjective
Explore 21 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICSChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Single Correct
Explore 107 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICSChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Exercise 4.1
Explore 23 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBook:CENGAGE PHYSICSChapter:KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSExercise:Interger
Explore 11 Videos
- MISCELLANEOUS KINEMATICSBook:CENGAGE PHYSICSChapter:MISCELLANEOUS KINEMATICSExercise:Interger type
Explore 3 Videos
Similar Questions
A simple pendulum of length l swings from a small angle θ . Its swinging is constrained by the smooth inclined planes OP and PC. Assuming elastic collision of the bob with the plane PC, find
a. angular amplitude for the motion of the bob in the left hand side of its mean position.
b. time period for a complete cycle of motion of the bob.

View SolutionA simple pendilum with bob of mass m and length l is held in position at an angle θ with t he verticle. Find its speed when it passes the lowest position.
View Solution
Knowledge Check
A simple pendulum of length l is set in motion such that the bob, of mass m, moves along a horizontal circualar path , and the string makes a constant angle θ with the vertical. The time period of rotation of the bob is l and the tension in the thread is T
At=2π√l/gBt=2π√lcosθ/gCT=4π2mlt2DThe bob is in equilibriumA simple pendulum of length L swings in a vertical plane. The tension of the string when it makes an angle θ with the vertical and the bob of mass m moves with a speed v is (g is the gravitational acceleration)
Amv2/LBmgcosθ+mv2/LCmgcosθ−mv2/LDmgcosθA simple pendulum has a length l & mass of bob m. The bob is given a charge q coulomb. The pendulum is suspended in a uniform horizontal electric field of strength E as shown in figure, then calculate the time period of oscillation when bob is slightly displaced from its mean position.
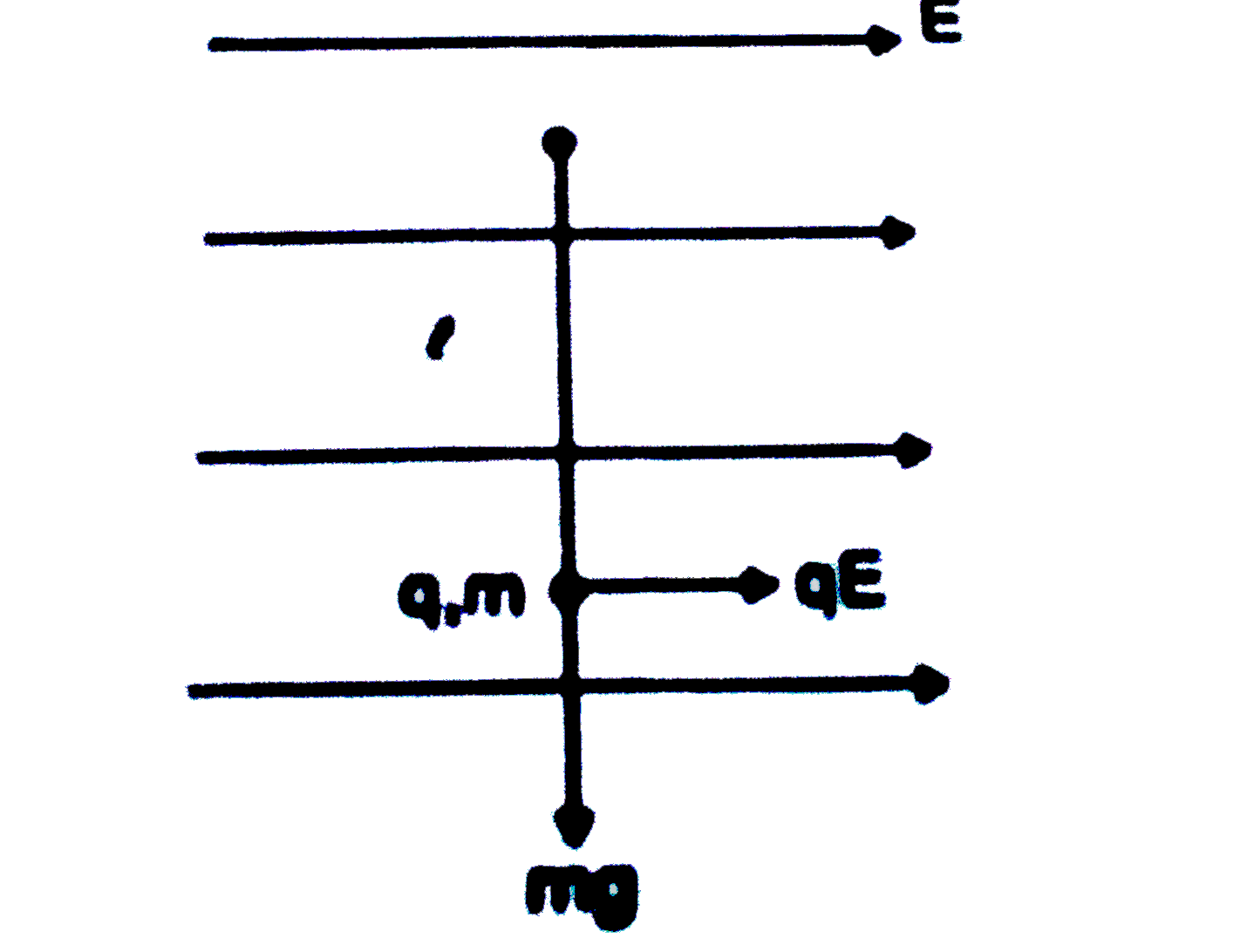 A2π√lgB2π ⎷⎧⎨⎩lg+qEm⎫⎬⎭C2π ⎷⎧⎨⎩lg−qEm⎫⎬⎭D2π ⎷l√g2+(qEm)2
A2π√lgB2π ⎷⎧⎨⎩lg+qEm⎫⎬⎭C2π ⎷⎧⎨⎩lg−qEm⎫⎬⎭D2π ⎷l√g2+(qEm)2
Show that for small oscillations the motion of a simple pendulum is simple harmonic. Derive an expression for its time period. Does it depend on the mass of the bob ?
View SolutionA bob of mass 2 kg hangs from a string of length 5 m . It swings from its rest position to one of the sides so that the string makes an angle of 60∘ with the vertical Calculate the gain in potential energy of the bob .
View SolutionA simple pendulum of length 40 cm oscillates with an angular amplitude of 0.04 rad. Find a. the time period b. the linear amplitude of the bob, c. The speed of the bob when the strig makes 0.02 rad with the vertical and d. the angular acceleration when the bob is in moemntary rest. Take g=10ms−2.
View SolutionThe bob of a pendulum of length l is pulled aside from its equilibrium position through an angle θ and then released. The bob will then pass through its equilibrium position with a speed v, where v equals
View SolutionA simple pendulum has a bob of mass m and swings with an angular amplitude ϕ. The tension in thread is T. At a certain time the string makes an angle θ with the vertical (θ≤ϕ)
View Solution

