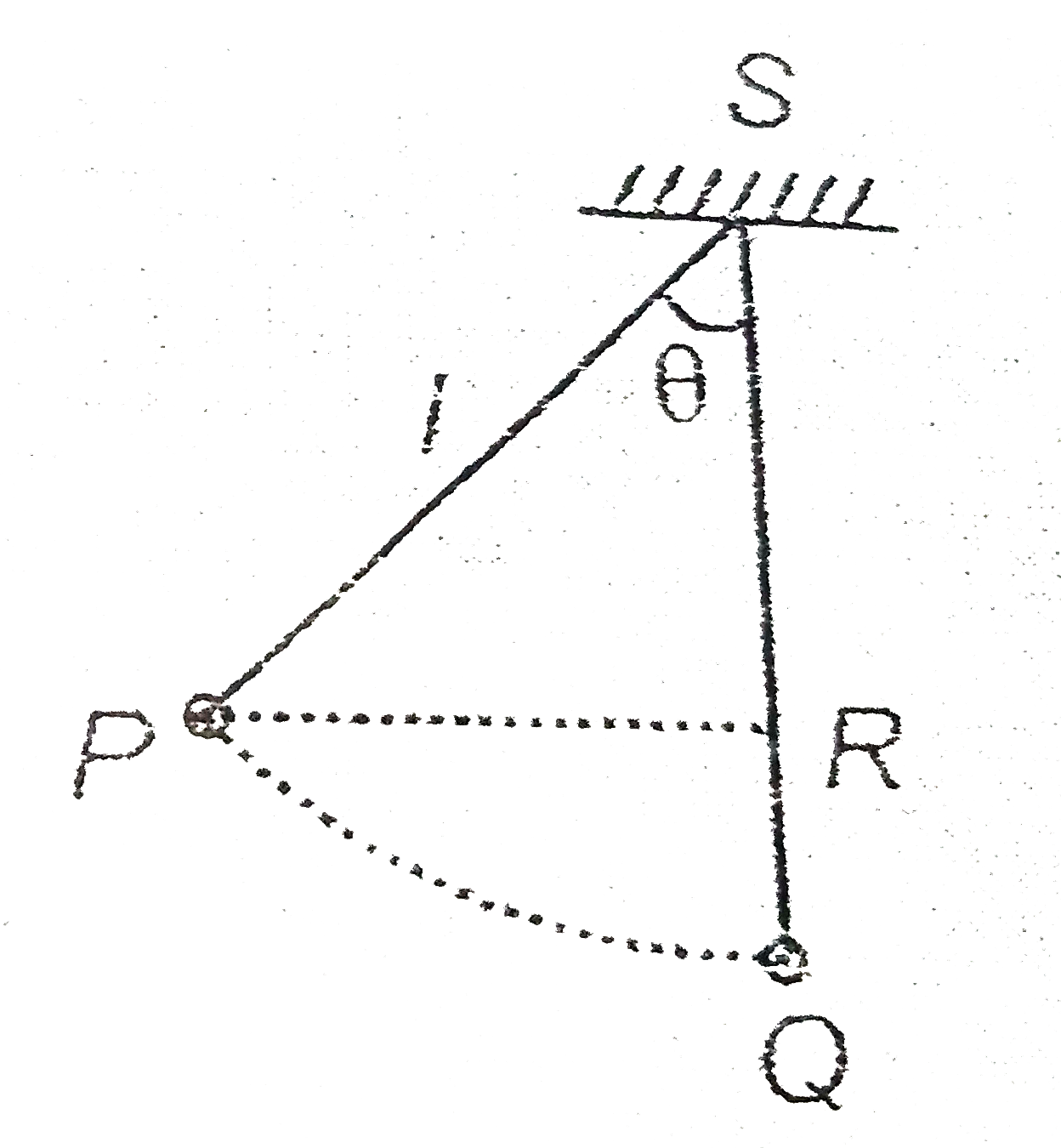
A simple pendilum with bob of mass m and length l is held in position at an angle θ with t he verticle. Find its speed when it passes the lowest position.
The height bob comes down is QR
h=QR=SQ=−SR=I−Icosθ
By law of conservation of mechanical energy
mgh=12mv2
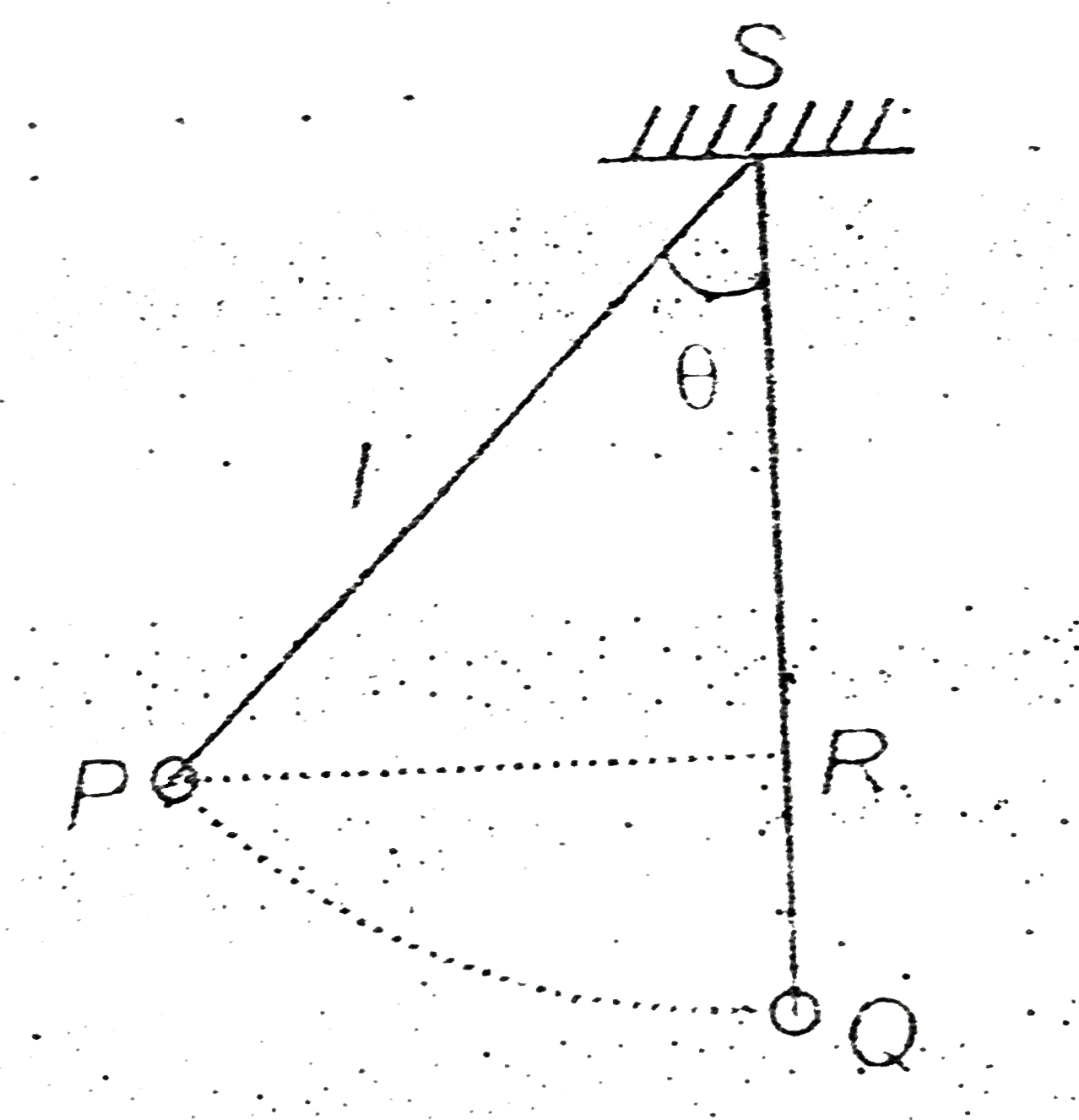
During motion of the bob from P to Q, its PE gets converted to KE. The height h, it comes in downward direction is QR
h=QR=SQ−SR=I−Icosθ.
By the law of conservation of mechanical energy
mgh=12mv2
mg(−lcosθ)=12mv2
v=√2gl(1−cosθ)
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTECHAPTER - WORK, ENERGY AND POWEREXERCISE - SECTION-A (OBJECTIVE TYPE QUESTIONS (ONE OPTIONISCORRECT)
60 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTECHAPTER - WORK, ENERGY AND POWEREXERCISE - SECTION-B (SUBJECTIVE TYPE QUESTIONS) (ONE OPTIONS IS CORRECT)
44 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTECHAPTER - WORK, ENERGY AND POWEREXERCISE - IILUSTRATION
2 Videos
- WAVESBOOK - AAKASH INSTITUTECHAPTER - WAVESEXERCISE - ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))
12 Videos
Similar Questions
A pendulum bob of mass m and length L is released from angle θ with the vertical. Find
(a) the speed of the bob at the bottom of the swing and
(b) tension in the string at that time
View SolutionA simple pendulum of length l and consisting of a ball of mass m is released from a position making an angle θ=cos−1 (0.8) with the vertical and strikes at its lowest position a block of mass M resting on a rough horizontal plane. If the coefficient of kinetic friction between the plane and the block is 0.2 find
(a) How long the block will move along the plane, if the ball of the pendulum rebounds to an angle β=cos−1 (0.9)A
(b) The coefficient of restitution, use Mm=10 and 1= 1 m
View Solution
Knowledge Check
A simple pendulum with bob of mass m and length x is held in position at an angle θ1 and then angle θ2 with the vertical. When released from these positions, speeds with which it passes the lowest postions are v1&v2 respectively. Then ,v1v2 is.
A1−cosθ11−cosθ2B√1−cosθ11−cosθ2C√2gx(1−cosθ1)1−cosθ2D√1−cosθ12gx(1−cosθ2)The bob of a pendulum of length l is pulled aside from its equilibrium position through an angle θ and then released. The bob will then pass through its equilibrium position with a speed v, where v equals
A√2glB√2gl(1+cosθ)C√2gl(1−cosθ)D√2gl(1+sinθ)A simple pendulum of bob mass m and length l is displaced from its mean position O to a point A and then released . If v is the velocity of the bob at O, h is the height of string of pendulum when bob passes through point O is /are (neglect friction )
A2mghlB2mg1+(h)lCmg1+(2h)lDmg1−(2h)l
The bob of pendulum of length l is pulled aside from its equilibrium position through an angle θ and then released. Find the speed v with which the bob passes through the equilibrium position.
View SolutionA pendulum has length L = 1.8 m. The bob is released from position shown in the figure. Find the tension in the string when the bob reaches the lowest position. Mass of the bob is 1 kg.

View SolutionA simple pendulum of length L swings in a vertical plane. The tension of the string when it makes an angle θ with the vertical and the bob of mass m moves with a speed v is (g is the gravitational acceleration)
View SolutionA bob hangs from a rigid support by an inextensible string of length l. It is released from rest when string makes an agngle 60∘ with vertical . The speed of the bob at the lowest position is
View SolutionA simple pendulum of mass m and length L is held in horizontal position. If it is released from this position, then find the angular momentum of the bob about the point of suspension when it is vertically below the point of suspension.
View Solution
