A smooth horizontal disc rotates about the vertical axis O (figure) with a constant angular velocity ω. A thin uniform rod AB of length l performs small oscillation about the vertical axis A fixed to the disc at a distance a from the axis of the disc. Find the frequency ω0 of these oscillations.

Let us go to the rotating frame, in which the disc is stationary. In this frame the rod is subjected to coriolis and centrigugal forces, Fcor and Fcf, where Fcor=∫2dm(v′×−→ω0) and Fcf=∫dmω20r, where r is the position of an elemental mass of the rod. with respect to point O ( disc's centre 0 and
v′=dr′dt
As, r=OP=OA+AP
So, drdt=d(AP)dt=v′ ( as OA is constant)
As the rod is vibrating transversely , so v′ is directeld perpendicular to the length of the rod. Hence 2dm(v′×→ω) for each elemental mass of the rod is directed along PA. Therefore the net torque about A becomes zero. The not torque of centrifulgal force about point A:
Now, →τcf(A)=∫AP×dmω20r=∫AP×(ml)dsω20(OA+AP)
=∫AP×(mlds)ω20OA=∫mldsω20sasinθ(−k)
=mlω20asinθ(−k)∫t0sds=mω20al2sinθ(−k)
So τcf(Z)=→τcf(A).k=−mω20al2sinθ
According to the equation of rotational dynamics :τA(Z)=lAαZ
or −mω20al2sinθ=ml23..θ
or ...θ=−32ω20alsinθ
Thus, for small θ, ..θ=−32ω20alsinθ
This implies that the frequency ω0 of oscillation is ω0=√3ω2a2l

Topper's Solved these Questions
- OSCILLATIONS AND WAVESBook:IE IRODOV, LA SENA & SS KROTOVChapter:OSCILLATIONS AND WAVESExercise:Electric Oscillations
Explore 56 Videos
- OSCILLATIONS AND WAVESBook:IE IRODOV, LA SENA & SS KROTOVChapter:OSCILLATIONS AND WAVESExercise:Elastic Waves
Explore 39 Videos
- OPTICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:OPTICSExercise:Exercise
Explore 2 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Relativistic Mechanics
Explore 49 Videos
Similar Questions
Find out the angular frequency of small oscillation about axis O
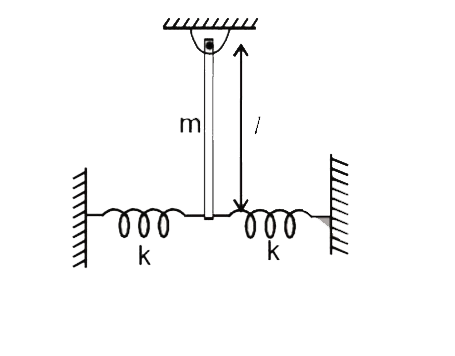
View SolutionA homogeneous disc of weight W and radius R rotates about the vertical axis OZ, the initial angular velocity being ω0. During the motion, the brake block A is pressed to the disc,with a radial force N for t0 seconds and the disc comes to rest because of friction. Find the coefficient of friction.
View Solution
Knowledge Check
A disc of radius R is pivoted at its rim. The period for small oscillations about an axis perpendicular to the plane of disc is
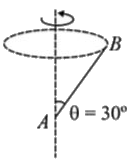
A2π√RgB2π√2RgC2π√2π3gD2π√3R2gA rod is rotating with angular velocity ω about axis AB. Find cosθ.
 Ag2lω2Bglω2C2g(lω)2D3g2lω2
Ag2lω2Bglω2C2g(lω)2D3g2lω2A rod AB of mass m and length l is rotating about a vertical axis as shown. It's moment of inertia about this axis is :
 Aml23Bml24Cml216Dml212
Aml23Bml24Cml216Dml212
A conducting disc of radius r rotates with a small but constant angular velocity ω about its axis. A uniform magnetic field B exists parallel to the axis of rotation. Find the motional emf between the centre and the periphery of the disc.
View SolutionA conical pendulum, a thin uniform rod of length l and mass m, rotates uniformly about a vertical axis with angular velocity ω(the upper end of the rod is hinged). Find the angle θ between the rod and the vertical.
View SolutionA thin uniform copper rod of length l and mass m rotates uniformly with an angular velocity ω in a horizontal plane about a vertical axis passing through one of its ends. Determine the tension in the rod as a function of the distance r from the rotation axis. Find the elongation of the rod.
View SolutionA smooth horizontal disc rotates with a constant angular velocity ω about a stationary vertical axis passing through its centre, the point O. At a moment t=0 a disc is set in motion from that:
point with velocity v0. Find the angular momentum M(t) of the disc relative to the point O in the reference frame fixed to the disc. Make sure that this angular momentum is caused by the Coriolis force.
View SolutionA horizontal disc rotating about a vertical axis passing through its centre makes 180 rpm. A small piece of wax of mass 10 g falls vertically on the disc and adheres to it at a distance of 8 cm from its axis. If the frequency is thus reduced to 150 rpm, calculate the moment of inertia of the disc.
View Solution

