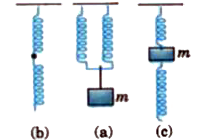
Two identical springs, each of spring factor k, may be connected in the following ways. Deduce the spring factor of the oscillation of the body in each case.
To solve the problem of finding the equivalent spring constant when two identical springs, each with spring constant k, are connected in different configurations, we can analyze each case step by step.
Case 1: Springs in Parallel
1. Understanding the Configuration: When two springs are connected in parallel, they both stretch by the same amount x when a force is applied.
2. Force Balance: The total force exerted by the springs can be expressed as:
F=T1+T2
where T1 and T2 are the tensions in the two springs.
3. Tension in Each Spring: Since both springs have the same spring constant k and stretch by the same amount x:
T1=kxandT2=kx
4. Total Force: Therefore, the total force is:
F=kx+kx=2kx
5. Equivalent Spring Constant: The equivalent spring constant keq can be defined as:
F=keqx
Setting the two expressions for force equal gives:
keqx=2kx
Dividing both sides by x (assuming x≠0):
keq=2k
Case 2: Springs in Series
1. Understanding the Configuration: When two springs are connected in series, the total extension x is the sum of the extensions of each spring.
2. Displacement of Each Spring: Let the displacement of the first spring be x1 and the second spring be x2. Thus:
x=x1+x2
3. Force Balance: The force in each spring is the same when they are in series, so:
T=kx1=kx2
4. Expressing Displacements: From the above, we can express x1 and x2 in terms of the force T:
x1=Tkandx2=Tk
5. Total Displacement: Substituting back into the total displacement gives:
x=Tk+Tk=2Tk
6. Equivalent Spring Constant: The equivalent spring constant keq can again be defined as:
T=keqx
Setting the two expressions for x equal gives:
T=keq(2Tk)
Dividing both sides by T (assuming T≠0):
1=2keqk
Rearranging gives:
keq=k2
Case 3: Single Spring
1. Understanding the Configuration: If there is only one spring, the equivalent spring constant is simply that of the single spring.
2. Equivalent Spring Constant: Thus:
keq=k
Summary of Results
- Case 1 (Parallel): keq=2k
- Case 2 (Series): keq=k2
- Case 3 (Single Spring): keq=k
1. Understanding the Configuration: When two springs are connected in parallel, they both stretch by the same amount x when a force is applied.
2. Force Balance: The total force exerted by the springs can be expressed as:
F=T1+T2
where T1 and T2 are the tensions in the two springs.
3. Tension in Each Spring: Since both springs have the same spring constant k and stretch by the same amount x:
T1=kxandT2=kx
4. Total Force: Therefore, the total force is:
F=kx+kx=2kx
5. Equivalent Spring Constant: The equivalent spring constant keq can be defined as:
F=keqx
Setting the two expressions for force equal gives:
keqx=2kx
Dividing both sides by x (assuming x≠0):
keq=2k
1. Understanding the Configuration: When two springs are connected in series, the total extension x is the sum of the extensions of each spring.
2. Displacement of Each Spring: Let the displacement of the first spring be x1 and the second spring be x2. Thus:
x=x1+x2
3. Force Balance: The force in each spring is the same when they are in series, so:
T=kx1=kx2
4. Expressing Displacements: From the above, we can express x1 and x2 in terms of the force T:
x1=Tkandx2=Tk
5. Total Displacement: Substituting back into the total displacement gives:
x=Tk+Tk=2Tk
6. Equivalent Spring Constant: The equivalent spring constant keq can again be defined as:
T=keqx
Setting the two expressions for x equal gives:
T=keq(2Tk)
Dividing both sides by T (assuming T≠0):
1=2keqk
Rearranging gives:
keq=k2
1. Understanding the Configuration: If there is only one spring, the equivalent spring constant is simply that of the single spring.
2. Equivalent Spring Constant: Thus:
keq=k
- Case 1 (Parallel): keq=2k
- Case 2 (Series): keq=k2
- Case 3 (Single Spring): keq=k
Topper's Solved these Questions
- OSCILLATIONSBook:SL ARORAChapter:OSCILLATIONSExercise:Type C Based on Oscillations of a Simple Pendulum
Explore 7 Videos
- OSCILLATIONSBook:SL ARORAChapter:OSCILLATIONSExercise:Type D Based on Other Examples of SHM
Explore 2 Videos
- OSCILLATIONSBook:SL ARORAChapter:OSCILLATIONSExercise:Exercise
Explore 233 Videos
- MOTION IN ONE DIMENSIONBook:SL ARORAChapter:MOTION IN ONE DIMENSIONExercise:problems for self practice
Explore 66 Videos
- Physical worldBook:SL ARORAChapter:Physical worldExercise:Exercise
Explore 49 Videos
Similar Questions
Two identical springs (springs constant K) are connected together in three different ways. In which case will the spring factor of the oscillation of the body be least ?
View SolutionTwo identical springs, each of force constant k are connected I (a) series (b) parallel and they support a mass M. Calculate the ratio of the frequency of oscillation of the mass in two systems.
View Solution
Knowledge Check
Two identical springs of spring constant k each are connected in series and parallel as shown in figure. A mass M is suspended from them. The ratio of their frequencies of vertical oscillation will be
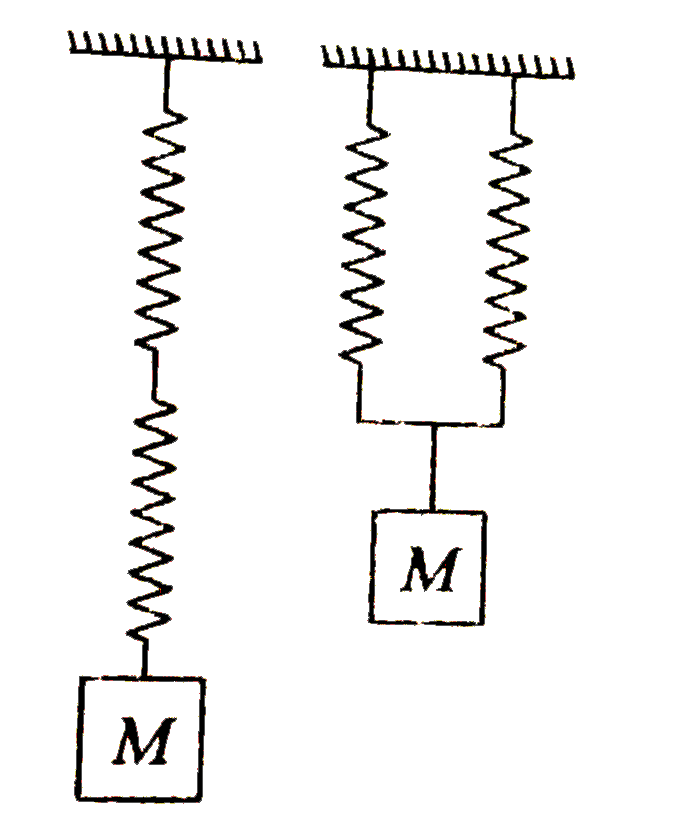 A1:2B2:1C4:1D1:4
A1:2B2:1C4:1D1:4A particle of mass m is attached to three identical massless springs of spring constant k as shown in the m 135 figure. The time period of vertical oscillation of the particle is
 A2π√mkB2π√m2kC2π√m3kDπ√mk
A2π√mkB2π√m2kC2π√m3kDπ√mkTwo springs of force constant k and 2k are connected to a mass shown in figure the frequency of oscillation of the mass is
 A12π√mkB12π√2kmC12π√3kmD12π√mk
A12π√mkB12π√2kmC12π√3kmD12π√mk
Two springs of force constant k and 2k are connected to a mass shown in figure the frequency of oscillation of the mass is

View SolutionTwo springs of spring constantsK1 and K2 are joined in series. The effective spring constant of the combination is given by
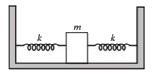
View SolutionA block of mass m is connected to two indentical springs of spring constant k which are in turn connected to fixed supports as shown in the figure. Find the time period for small oscillations of the block.
View SolutionOn a smooth inclined plane a body of mass M is attached between two springs. The other ends of the spring are fixed to ffirm supports. If each spring has a force constant k, the period of oscillation of the body is: (assuming the spring as massless)

View SolutionOn a smooth inclined plane, a body of mass M is attached between two springs. The other ends of the springs are fixed to firm supports. If each spring has force constant K , the period of oscillation of the body (assuming the springs as massless) is

View Solution

