A rod PQ of length L revolves in a horizontal plane about the axis YY´. The angular velocity of the rod is w. If A is the area of cross-section of the rod and ρ be its density, its rotational kinetic energy is
13AL3ρω2
12AL3ρω2
124AL3ρω2
118AL3ρω2
The correct Answer is:C
If rotation axis is passing through its middle point & is ⊥ to its plane, then moment of inertia about YY. is
I=ML212
where M = volume × density = (L×A)×ρ
so, I=L3Aρ12
so rotational K.E.=12Iω2=L3Aρω224

Topper's Solved these Questions
- SYSTEM OF PARTICLES & ROTATIONAL MOTION BOOK - DISHA PUBLICATIONCHAPTER - SYSTEM OF PARTICLES & ROTATIONAL MOTION EXERCISE - EXERCISE-2 : CONCEPT APPLICATOR
28 Videos
- SYSTEM OF PARTICLES & ROTATIONAL MOTION BOOK - DISHA PUBLICATIONCHAPTER - SYSTEM OF PARTICLES & ROTATIONAL MOTION EXERCISE - EXERCISE-2 : CONCEPT APPLICATOR
28 Videos
- SEMICONDUCTOR ELECTRONICS : METERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - DISHA PUBLICATIONCHAPTER - SEMICONDUCTOR ELECTRONICS : METERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - EXERCISE -2: CONCEPT APPLICATOR
25 Videos
- THERMAL PROPERTIES OF MATTER BOOK - DISHA PUBLICATIONCHAPTER - THERMAL PROPERTIES OF MATTER EXERCISE - Exercise-2 (Concept Applicator)
28 Videos
Similar Questions
A rod PQ of length L revolves in a horizontal plane about the axis YY´. The angular velocity of the rod is w. If A is the area of cross-section of the rod and r be its density, its rotational kinetic energy is
View SolutionA uniform material rod of length L is rotated in a horizontal plane about a vertical axis through one of its ends. The angular speed of rotation is w. Find increase in length of the rod. It is given that density and Young’s modulus of the rod are r and Y respectively.
View Solution
Knowledge Check
The dimensions of lKA are (l is the length of rod, K is the thermal conductivity of rod and A is the area of cross-section of rod)
A[ML2T−3K−1]B[M−1L−2T3K]C[ML2T−3K−2]D[MLT−3K−1]A rod having length L, density D and area of Cross-section A is rotating about the centre with velocity @ and perpendicular to its length. Its rotational kinetic energy is
A13DAL3ω2B112DAL3ω2C124DAL3ω2D16DAL3ω2A uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
A12mω2xB12mω2(1−x2l)C12mω2l(1−x2l2)D12mω2l[1−xl]
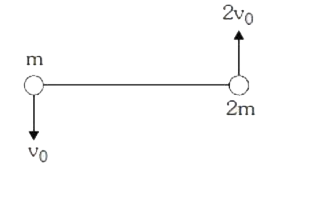
Two point masses of mass m and 2m placed on smooth horizontal plane are connected by a light rod of length l. Masses are given velocities in horizontal plane perpendicular to rod as shown. If area of cross section of rod is A and Young's modulus is Y, then elongation in the rod, will be
View SolutionA smooth rod of length l rotates freely in a horizontal plane with the angular velocity about a stationary vertical axis O as shown in Fig. The moment of inertia of the rod is equal to I relative to the axis. A small ring of mass m is located on the rod close to the rotation axis and is tied to it by a thread. When the thread is burned, the ring starts sliding radially outwards along the rod. Find the velocity v of the ring relative to the rod as a function of its distance r from the rotation axis.
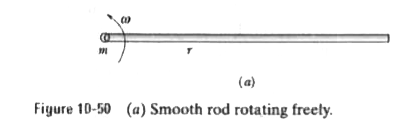
View SolutionA rod PQ of length l is rotating about end P, with an angular velocity ω. Due to electrifugal forceed the free electrons in the rod move toward the end Q and an emf is created. Find the induced emf.

View SolutionA uniform rod of length L rests on a frictionless horizontal surface. The rod is pivoted about a fixed frictionless axis at one end. The rod is initially at rest. A bulled travelling parallel to the horizontal surface and perpendicular to the rod with speed v strikes the rod at its centre and becomes embedded in it. the mass of the bullet is one-sixth the mass of the rod.
(a). What is the final angular velocity of the rod?
(b). What is the ratio of the kinetic energy of the system after the collision to the kinetic energy of te bullet the o collision?
View SolutionA uniform rod of mass m and length L lies radialy on a disc rotating with angular speed ω in a horizontal plane about vertical axis passing thorugh centre of disc. The rod does not slip on the disc and the centre of the rod is at a distance 2L from the centre of the disc. them the kinetic energy of the rod is

View Solution
