The function f(x)=∫x−1t(et−1)(t−1)(t−2)3(t−3)5dt has a local minimum at x= 0 (b) 1 (c) 2 (d) 3
A
0
B
1
C
2
D
3
Video Solution
Text Solution
The correct Answer is:B, D
f(x)=∫x−1t(et−1)(t−1)(t−2)3(t−3)5dt

f'(x)=ddx∫x−1t(et−1)(t−1)(t−2)3(t−3)5dt
=x(ex−1)(x−1)(x−2)3(x−3)5×1
[∵ddx∫ψ(x)ϕ(x)f(t)dt=f{ψ(x)}ψ'(x)−f(ϕ(x)}ϕ'(x)]
For local minimum, f'(x)=0
⇒ x=0,1,2,3
Let f'(x)=g(x)=x(ex−1)(x−1)(x−2)3(x−3)5
Using sign rule,
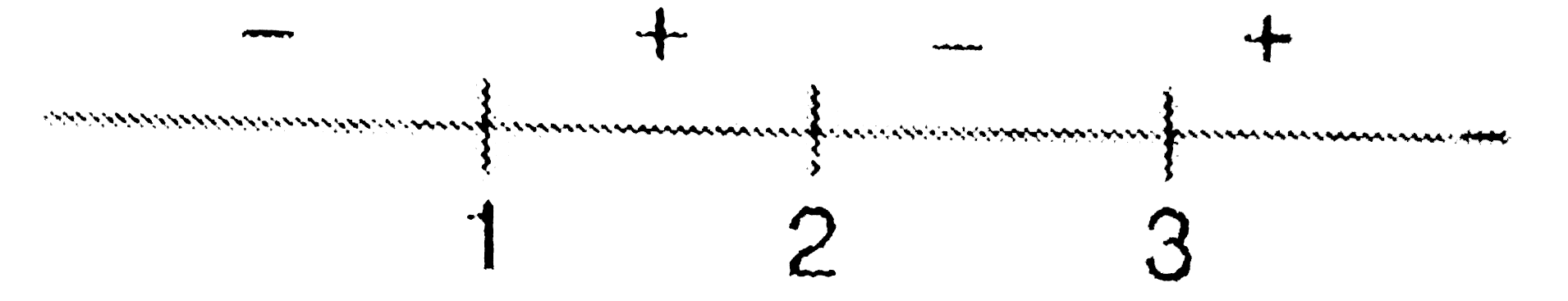
This shows that f(x) has a local minimum at x=1andx=3 and maximum at x=2
Therefore, (b) and (d) are the correct answers.
|
Topper's Solved these Questions
- APPLICATION OF DERIVATIVES Book:IIT JEE PREVIOUS YEARChapter:APPLICATION OF DERIVATIVES Exercise:MAXIMA AND MINIMA (MATCH THE COLUMNS)
Explore 1 Video
- APPLICATION OF DERIVATIVES Book:IIT JEE PREVIOUS YEARChapter:APPLICATION OF DERIVATIVES Exercise:MAXIMA AND MINIMA (PASSAGE BASED PROBLEMS)
Explore 3 Videos
- APPLICATION OF DERIVATIVES Book:IIT JEE PREVIOUS YEARChapter:APPLICATION OF DERIVATIVES Exercise:MAXIMA AND MINIMA (OBJECTIVE QUESTIONS I)
Explore 29 Videos
- 3D GeometryBook:IIT JEE PREVIOUS YEARChapter:3D GeometryExercise:Equation of Plane Objective Question II (Integer Answer Type Question)
Explore 1 Video
- AREABook:IIT JEE PREVIOUS YEARChapter:AREAExercise:AREA USING INTEGRATION
Explore 55 Videos
Similar Questions
Knowledge Check
The function f(x)=∫x−1t(et−1)(t−1)(t−2)3(t−3)5dt has a local minimum at x= 0 (b) 1 (c) 2 (d) 3
A0B1C2D3if f(x)=∫x−1t(et−1)(t−1)(t−2)3(t−3)5dthas a local minimum then sum of values of x
A1B3C4D5The function F(x)=∫x0log(1−t)1+tdt is
Aan even functionBan odd functionCa periodic functionDnone of these
The value of
sin2x∫0sin−1√tdt+cos2x∫0cos−1√tdt, is
View SolutionLet f(x)=∫x0(t−1)(t−2)2dt, then find a point of minimum.
View SolutionLet f(x)=∫x0et(t−1)(t−2)dt. Then, f decreases in the interval
View SolutionThe function
f(x)=∫x1{2(t−1)(t−2)3+3(t−1)2(t−2)2}dt attains its maximum at x =
View Solutionf(x)=∫x0t(t−1)(t−2)dt takes on its minimum values of x =
View Solution