Question

The function $f\left(x\right)=2\left|x\right|+|x+2|=\left|\left|x\right|2\right|-2\left|x\right|\mid$
has a local minimum or a local maximum at $x=$

$-2$
(b) $-\frac{2}{3}$
(c) 2
(d) $\frac{2}{3}$

Options

A. `-2 `
B. `(-2)/(3)`
C. ` 2`
D. ` 2//3`

Answer

A::D

Explanation

We know that, ` |x| = {{:(x",",, if x ge0 ),( - x",",, if x lt 0 ):}`
`rArr " " |x- a| = {{:(x- a",",, if x ge a), ( - (x - a)"," ,, if x lt a):}`
and for non - differentiable continuous function, the maximum or minimum can be checked with graph as


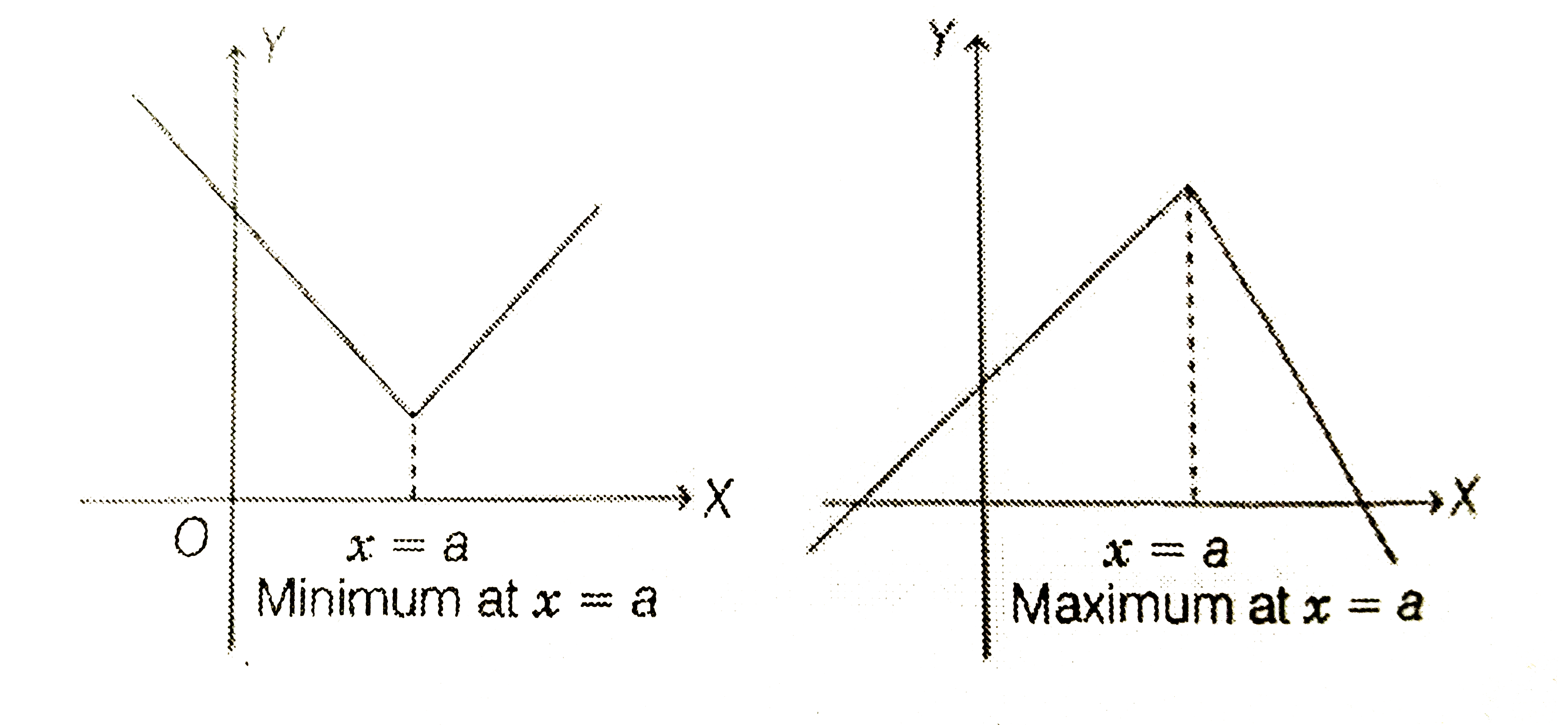
Here, `f(x) = 2 |x| + |x + 2| - ||x + 2| - 2 |x||`
`= {{:( - 2x - (x +2) + (x - 2)",",, if when x le - 2 ), ( - 2 x +x +2 + 3x + 2 ",",, if when - 2 lt x le - 2//3 ),( - 4x ",",, if when - (2)/(3) lt x le 0), ( 4x ",",, if when 0 lt x le 2 ), ( 2x + 4",",, if when x gt 2):}`
`= {{:( - 2 x - 4",",, if ,, x le - 2), ( 2x - 4",",, if ,, -2 lt x le - 2//3), ( - 4x ",",, if ,, - (2)/(3) lt x le 0 ), ( 4x",",, if ,, 0 lt x le 2), ( 2x + 4"," ,, if ,, x gt 2):}`
Graph for `y = f (x)` is shown as