A monochromatic beam of light is incident at 60∘ on one face of an equilateral prism of refractive inder n and emerges from the opposite face making an angle θ with the normal. For n=√3, the value of θ is 60∘anddθdn=m. The value of m is.
The correct Answer is:2
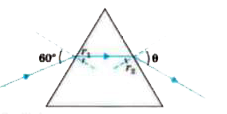
Applying Snell.s law
⇒1×sin60=n×sinr1
⇒sinr1=√32n
⇒cosr1=12n√4n2−3 ….(1)
μsinθ=const
⇒n×sinr2=1×sinθ
⇒sinθ=nsinr2
⇒sinθ=nsin(50−r1)
⇒sinθ=n[sin60cosr1−cos60sinr1]
⇒sinθ=n[√32cosr1−12sinr1]
⇒sinθ=n×[√32×12n√4n2−3−n×12×√32n]
⇒sinθ√34√4n2−3−√34
On differentiating both the sides we get the following :
⇒cosθ×dθdn=√34×8n2√4n2−3
Now substituting n=√3 and θ=60∘.
⇒cos60×dθdn=√34×8√36
⇒12×dθdn=√34×8√36
⇒dθdn=2
Hence answer is 2.
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - CHAPTER PRACTICE TEST
14 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - OBJECTIVE TYPE QUESTIONS (MATRIX MATCH TYPE QUESTIONS)
1 Videos
- NUCLEIBOOK - MODERN PUBLICATIONCHAPTER - NUCLEIEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
15 Videos
- SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS BOOK - MODERN PUBLICATIONCHAPTER - SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS EXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
12 Videos
Similar Questions
A ray of light incident normally on the first face of a glass prism of refractive index 1.6 just emerges from the other face. Find the angle of the prism.
View SolutionA monochromatic beam of light is incident at the interface of two materials of refractive index n1 and n2 as shown . If n1>n2 and θC is the critical angle then which of the following statements is NOT true ?
View Solution
Knowledge Check
A beam of monochromatic light is incident at i=50∘ on one face of an equilateral prism, the angle of emergence is 40∘, then the angle of minimum deviation is :
A30∘B<30∘C≤30∘D≥30∘A ray of light is incident normally on one face of an equilateral prism of refractive index 1.5. The angle of deviation is: (Given sin−1.23=42∘)
A30∘B45∘C60∘D75∘If a light ray incidents normally on one of the faces of the prism of refractive index 2 and the emergent ray just grazes the second face of the prism, then the angle of deviation is
A0∘B30∘C45∘D60∘
A ray of light is incident at 60∘ on one face of a prism of angle 30∘ and the emergent ray makes 30∘ with the incident ray. The refractive index of the prism is
View SolutionA ray of light is incident normally on one of the equal faces of a right isosceles prism of refractive index 1.5. The angle between incident and emergent rays is
View SolutionFor an angle of incidence θ on an equilateral prism of refractive index √3, the ray refracted is parallel to the base inside the prism. The value of θis
View SolutionLight falls at normal incidence on one face of a glass prism of refractive index √2. Then the angle of emergence when the angle of the prism is 45∘
View SolutionA ray of light is incident at an angle of 60∘ on one face of a prism of angle 30∘. The ray emerging out of the prism makes an angle of 30∘ with the incident ray. The emergent ray is
View Solution
