Question

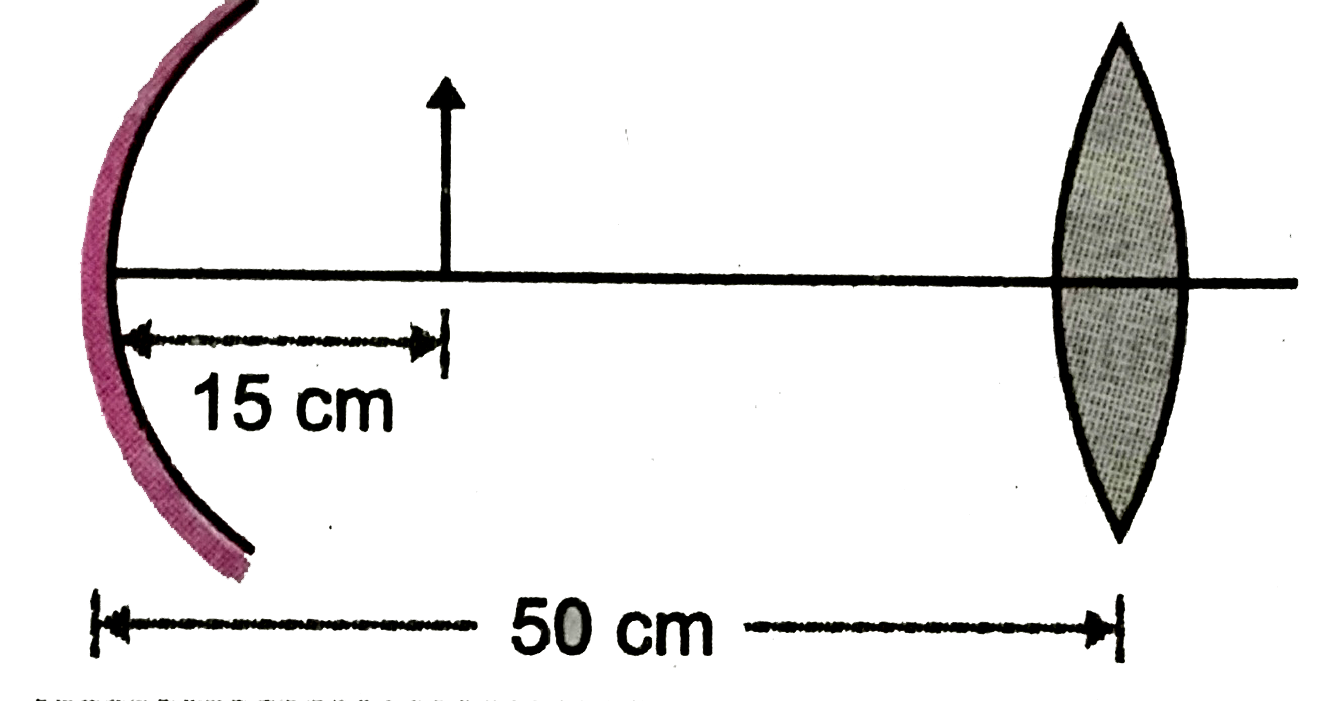
Consider a concave mirror and a convex lens (refractive index 1.5) of focal length $10cm$ each separated by a distance of $50cm$ in air (refractive index = 1) as shown in the Fig. An object is placed at a distance of $15cm$ from the mirror. Its erect image formed by this combination has magnification $M_1$. When this set up is kept in a medium of refractive index $7/6$, the magnification becomes $M_2$. The magnitude $\left(\frac{M_2}{M_1}\right)$ is :
.

Answer

7

Explanation

First we can apply mirror formula to find the location of image formed by mirror and this location is independent of surrounding material medium. So it will remain same in both the cases.
`(1)/(f) = (1)/(v) + (1)/(u) rArr (1)/(-10) = (1)/(v) + (1)/(-15)`
`rArr (1)/(v) = (1)/(15) - (1)/(10) = (2-3)/(30)`
`rArr v = -30 cm`
Hence image by mirror is at a distance 20 cm from the lens.
Applying lens formula in air we get the following :
`(1)/(f) = (1)/(v) - (1)/(u) rArr (1)/(10) = (1)/(v) - (1)/(-20)`
`rArr v = 20 cm`
`m = v//u = -1`
Note that overall magnification is multiplication of magnification produced by lens mirror. But here in both the cases magnification of mirror is same and hence ratio of the magnification achieved by the lens two cases will be the answer.
magnitude of magnification of lens in the first case is `m_(1) = 1`
To the find magnification in the second case we need to first find changed focal length when liquid is there in the surrounding.
`((1)/(10))/((1)/(f)) =((1.5-1)((1)/(R_(1))-(1)/(R_(2))))/(((1.5)/(7//6)-1)((1)/(R_(1))-(1)/(R_(2))))`
On solving we get `f = 3.5//2 cm`.
Applying lens formula we get the following :
`(1)/(f) = (1)/(v) - (1)/(u) rArr (2)/(35) = (1)/(v) - (1)/(20)`
`rArr (1)/(v) = (2)/(35) - (1)/(20) = (8-7)/(140)`
`rArr v = 140 cm`
`m_(2) = v//u = 140//(-20) = -7`
Ratio of the magnitudes of magnification
`M_(2)//M_(1) = (2 xx 7)/(2 xx 1) = 7`
Hence answer is 7.