There is a concave mirror of radius of curvature 20cm. A point object is placed at distance 15cm from the mirror. If point object start moving with speed 2mm/s perpendicular to principal axis then at this instant what will be the speed of image in mm/s ?
|0123456789|
The correct Answer is:4
To solve the problem step by step, we will use the mirror formula and the concept of magnification.
Step 1: Determine the focal length of the concave mirror.
The radius of curvature (R) is given as 20 cm. The focal length (f) is given by the formula:
f=R2
Substituting the value of R:
f=20 cm2=10 cm
Since it is a concave mirror, the focal length is negative:
f=−10 cm
Hint: Remember that for concave mirrors, the focal length is negative.
Step 2: Use the mirror formula to find the image distance (v).
The mirror formula is given by:
1f=1v+1u
Where:
- f is the focal length,
- v is the image distance,
- u is the object distance (which is negative for real objects).
Given that the object is placed at a distance of 15 cm from the mirror, we have:
u=−15 cm
Substituting the values into the mirror formula:
1−10=1v+1−15
Rearranging gives:
1v=1−10+115
Finding a common denominator (30):
1v=−330+230=−130
Thus:
v=−30 cm
Hint: Make sure to keep track of the signs when using the mirror formula.
Step 3: Calculate the magnification (m).
The magnification (m) is given by:
m=−vu
Substituting the values of v and u:
m=−−30−15=−2
Hint: Magnification tells you the ratio of the height of the image to the height of the object and its sign indicates the orientation of the image.
Step 4: Relate the velocities of the object and image.
The velocity of the image (vi) is related to the velocity of the object (vo) by the formula:
vi=m⋅vo
Given that the speed of the object is vo=2 mm/s:
vi=−2⋅2=−4 mm/s
Hint: The negative sign indicates the direction of the image's movement relative to the object.
Step 5: Conclusion
The speed of the image is 4 mm/s in the opposite direction to the movement of the object.
Final Answer: The speed of the image is 4 mm/s.
The radius of curvature (R) is given as 20 cm. The focal length (f) is given by the formula:
f=R2
Substituting the value of R:
f=20 cm2=10 cm
Since it is a concave mirror, the focal length is negative:
f=−10 cm
The mirror formula is given by:
1f=1v+1u
Where:
- f is the focal length,
- v is the image distance,
- u is the object distance (which is negative for real objects).
u=−15 cm
1−10=1v+1−15
Rearranging gives:
1v=1−10+115
Finding a common denominator (30):
1v=−330+230=−130
Thus:
v=−30 cm
The magnification (m) is given by:
m=−vu
Substituting the values of v and u:
m=−−30−15=−2
The velocity of the image (vi) is related to the velocity of the object (vo) by the formula:
vi=m⋅vo
Given that the speed of the object is vo=2 mm/s:
vi=−2⋅2=−4 mm/s
The speed of the image is 4 mm/s in the opposite direction to the movement of the object.
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - CHAPTER PRACTICE TEST
14 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - OBJECTIVE TYPE QUESTIONS (MATRIX MATCH TYPE QUESTIONS)
1 Videos
- NUCLEIBOOK - MODERN PUBLICATIONCHAPTER - NUCLEIEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
15 Videos
- SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS BOOK - MODERN PUBLICATIONCHAPTER - SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS EXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
12 Videos
Similar Questions
There is a concave mirror of focal length f and an object of length 2.5 cm is placed at a distance 1.5 f from concave mirror. Length of the object is perpendicular to the principal axis. What is the length of image in cm ?
|0123456789|
View SolutionA mirror of radius of curvature 20cm and an object which is placed at a distance of 15cm are both moving with velocities 1ms−1 and 10ms−1 as shown in Fig. Fing the velocity of image at this situation.
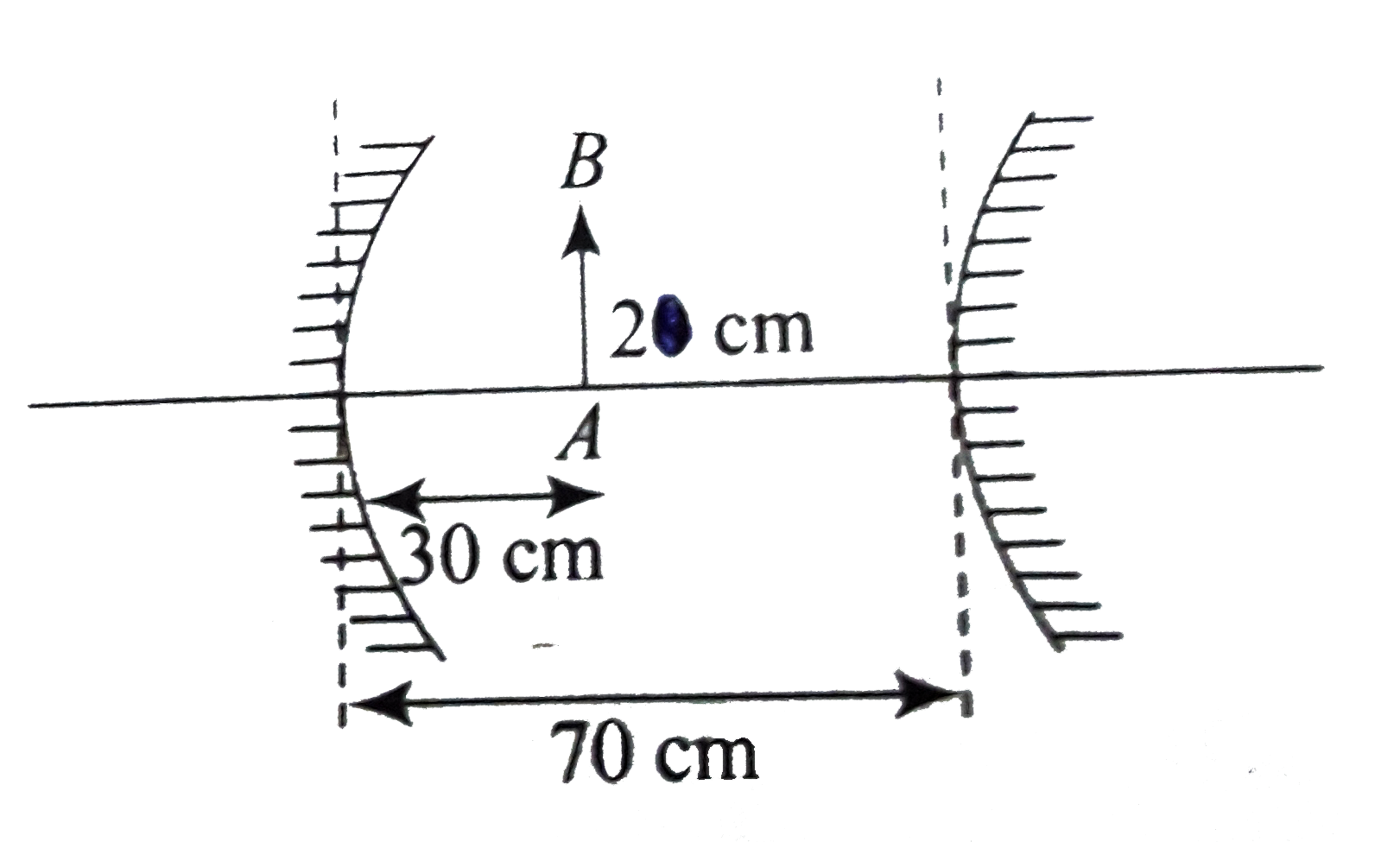
View Solution
Knowledge Check
A convex mirror has radius of curvature of 20 cm. An object is placed at such a distance from the mirror that the size of image is exactly half that of the object. The object must be at :-
A20cmB30cmC10cmD40cmA convex mirror has radius of curvature of 20 cm. An object is placed at such a distance from the mirror that the size of image is exactly half that of the object. The object must be at :-
A20 cmB30 cmC10 cmD40 cmAn object is present on the principal axis of a concave mirror at a distance 30cmfrom it.Focal length of mirror is20cm

If object starts moving with 2cms−1perpendicular to principal axis above the principal axis then,Aimage moves with velocity4cms−1below the principal axis.Bimage moves with velocity4cms−1above the principal axis.Cimage moves with velocity8cms−1below the principal axis.Dimage moves with velocity8cms−1above the principal axis.
A concave mirror has a focal length of 5 cm. When an object is placed at a distance of 15 cm from the mirror, then the image is formed in front of the mirror at ____cm.
View SolutionA point object on the principal axis at a distance 1.5cm in front of a concave mirror of radius of curvature 20cm has velocity ,2mm/s perpendicular to , the principal axis.The velocity of image at that instant will be
View SolutionAn object is present on the principal axis of a concave mirror at a distance 30cm from it. Focal length of mirror is 20cm.
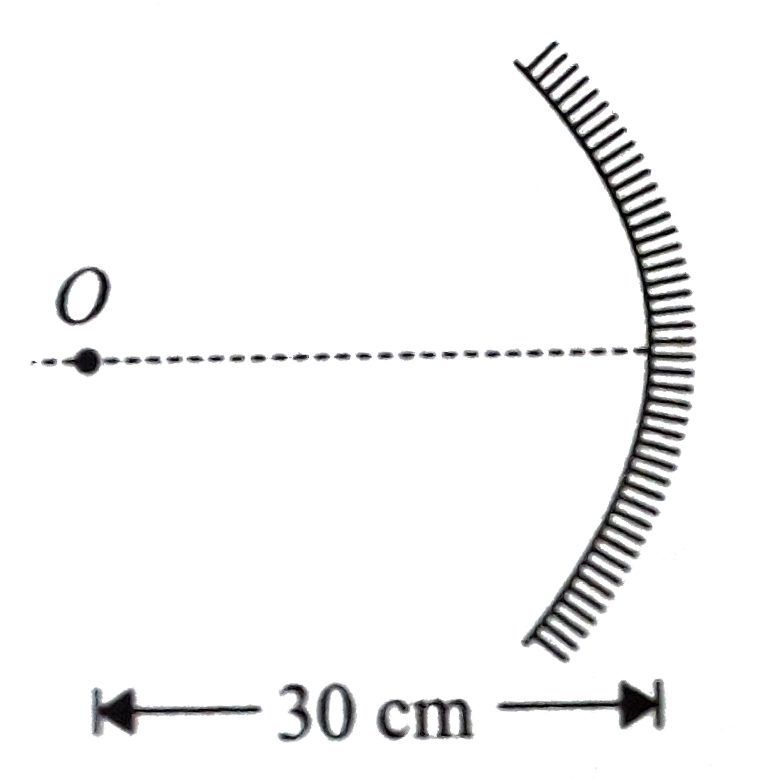
Q. If object starts moving with 2cms−1 perpendicular to principal axis above the principal axis then,
View SolutionA point object 'O' is at the center of curvature of a concave mirror. The mirror starts to move at a speed u, iin a direction perpendicular to the principal axis. Then, the initial velocity of the image is
View SolutionImage formed by a concave mirror radius of curvature 40 cm is half the size of the object. Then distance of object and its image from the mirror will be -
View Solution
