Light falls at normal incidence on one face of a glass prism of refractive index √2. Then the angle of emergence when the angle of the prism is 45∘
45°
60°
15°
90°
The correct Answer is:D
To solve the problem, we need to find the angle of emergence when light falls normally on one face of a glass prism with a refractive index of √2 and an angle of the prism of 45∘.
1. Understanding the Setup:
- The light ray falls normally on one face of the prism. This means that the angle of incidence i=0∘.
- The angle of the prism A=45∘.
2. Refraction at the First Face:
- Since the light is incident normally, it will pass through the first face without bending. Therefore, the angle of refraction R1=0∘.
3. Using the Prism Formula:
- For a prism, the relationship between the angle of the prism A, the angle of refraction R1, and the angle of refraction R2 at the second face is given by:
A=R1+R2
- Substituting the known values:
45∘=0∘+R2⟹R2=45∘
4. Applying Snell's Law at the Second Face:
- We apply Snell's law at the second face of the prism:
n1sinR2=n2sinE
- Here, n1=√2 (the refractive index of the prism), n2=1 (the refractive index of air), and R2=45∘.
- Substituting the values:
√2sin(45∘)=1sinE
- Since sin(45∘)=1√2:
√2⋅1√2=sinE⟹1=sinE
5. Finding the Angle of Emergence:
- The angle E such that sinE=1 is:
E=90∘
Final Answer:
The angle of emergence E is 90∘.
---
- The light ray falls normally on one face of the prism. This means that the angle of incidence i=0∘.
- The angle of the prism A=45∘.
- Since the light is incident normally, it will pass through the first face without bending. Therefore, the angle of refraction R1=0∘.
- For a prism, the relationship between the angle of the prism A, the angle of refraction R1, and the angle of refraction R2 at the second face is given by:
A=R1+R2
- Substituting the known values:
45∘=0∘+R2⟹R2=45∘
- We apply Snell's law at the second face of the prism:
n1sinR2=n2sinE
- Here, n1=√2 (the refractive index of the prism), n2=1 (the refractive index of air), and R2=45∘.
- Substituting the values:
√2sin(45∘)=1sinE
- Since sin(45∘)=1√2:
√2⋅1√2=sinE⟹1=sinE
- The angle E such that sinE=1 is:
E=90∘
The angle of emergence E is 90∘.
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRAUMENTS BOOK - NARAYNACHAPTER - RAY OPTICS AND OPTICAL INSTRAUMENTS EXERCISE - EXERCISE - 1 (C.W)(DISPERSION BY A PRISM)
4 Videos
- RAY OPTICS AND OPTICAL INSTRAUMENTS BOOK - NARAYNACHAPTER - RAY OPTICS AND OPTICAL INSTRAUMENTS EXERCISE - EXERCISE - 1 (C.W)(DEFECTS OF THE EYE)
3 Videos
- RAY OPTICS AND OPTICAL INSTRAUMENTS BOOK - NARAYNACHAPTER - RAY OPTICS AND OPTICAL INSTRAUMENTS EXERCISE - EXERCISE - 1 (C.W)(LENSES)
10 Videos
- NUCLEI BOOK - NARAYNACHAPTER - NUCLEI EXERCISE - ASSERTION & REASON
5 Videos
- SEMI CONDUCTOR DEVICESBOOK - NARAYNACHAPTER - SEMI CONDUCTOR DEVICESEXERCISE - Level-II (H.W)
36 Videos
Similar Questions
Light falls at normal incidence on one face of a glass prism of refractive index 1.5, what will be the angle of emergence when the angle of the prism is (a) 30∘ (b) 50∘ ?
View SolutionCalculate the angle of emergence (e) of the ray of light incident normally on the face AC of a glass prism ABC of refractive index √3. How will the angle of emergence change qualitatively, if the ray of light emerges from the prism into a liquid of refractive index 1.3 instead of air ?
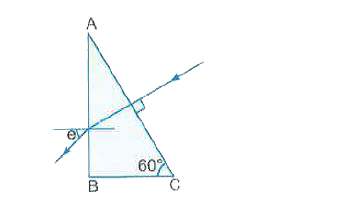
View Solution
Knowledge Check
A ray of light undergoes deviation of 30∘ when incident on an equilateral prism of refractive index √2. The angle made by the ray inside the prism with the base of the prism is
A15∘B0∘C45∘D30∘A ray of light is incident normally normallyh on one of the faces of a prism of apex angle 30∘ and refractive index √2. The angle of deviation of the ray is ________________ degrees.
A15∘B30∘C45∘D60∘A ray of light suffers a minimum deviation when incident on an equilateral prism of refractive index √2 The angle of incidence is
A30∘B45∘C60∘D50∘
A ray of light incident normally on the first face of a glass prism of refractive index 1.6 just emerges from the other face. Find the angle of the prism.
View SolutionA light ray falls perpendicular on one face of an equilateral prism having refractive index √2 .The angle of deviation is :
View SolutionA ray of light is incident normally normallyh on one of the faces of a prism of apex angle 30∘ and refractive index √2. The angle of deviation of the ray is ________________ degrees.
View SolutionIf a light ray incidents normally on one of the faces of the prism of refractive index 2 and the emergent ray just grazes the second face of the prism, then the angle of deviation is
View SolutionA ray of monochromatic light is incident on the refracting face of a prism (angle 75∘0 . It passes through the prism and is incident on the other face at the critical angle. If the refractive index of the prism is √2 , then the angle of incidence on the first of the prism is
View Solution
