Question

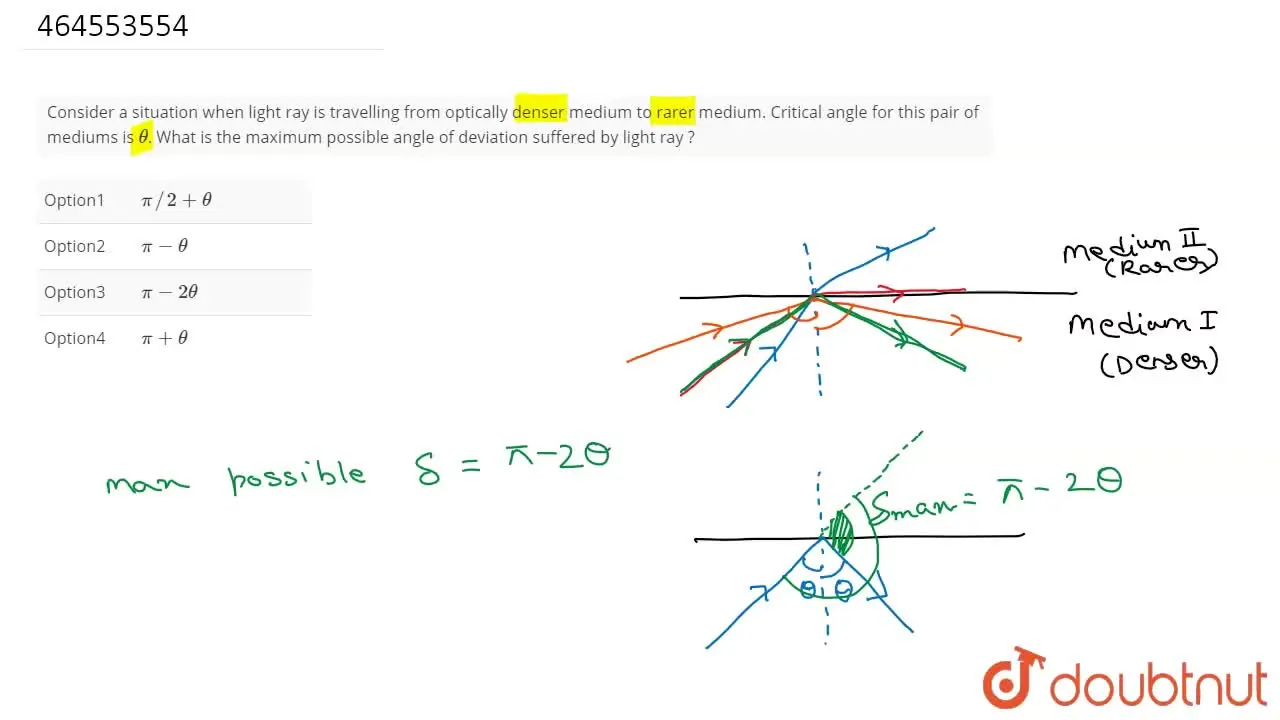
Consider a situation when light ray is travelling from optically denser medium to rarer medium. Critical angle for this pair of mediums is $\theta$. What is the maximum possible angle of deviation suffered by light ray ?

Options

A. `pi//2+theta`
B. `pi-theta`
C. `pi-2theta`
D. `pi+theta`

Answer

C

Explanation

To find the maximum possible angle of deviation suffered by a light ray traveling from an optically denser medium to a rarer medium, we can follow these steps:

1. Understanding the Critical Angle:
- The critical angle (θ) is defined as the angle of incidence in the denser medium at which the refracted ray in the rarer medium travels along the boundary (i.e., at 90 degrees to the normal).
- Beyond this angle, total internal reflection occurs.

2. Visualizing the Scenario:
- Draw a diagram with two media: medium 1 (denser) and medium 2 (rarer).
- Mark the interface and draw the incident ray making an angle θ (the critical angle) with the normal.

3. Identifying Total Internal Reflection:
- When the angle of incidence exceeds the critical angle, the light ray reflects back into the denser medium.
- The angle of reflection will equal the angle of incidence (θ).

4. Calculating the Maximum Angle of Deviation:
- The maximum deviation occurs when the light ray is incident at an angle just above the critical angle.
- The total deviation (Δ) can be calculated as the difference between the original path of the light ray and its final reflected path.
- The total angle around the normal at the interface is 180 degrees (π radians).

5. Finding the Deviation:
- The deviation can be expressed as:
\( \Delta_{\text{max}} = 180^\circ - 2\theta \)
- In radians, this can be written as:
\( \Delta_{\text{max}} = \pi - 2\theta \)

6. Conclusion:
- Therefore, the maximum possible angle of deviation suffered by the light ray is:
\( \Delta_{\text{max}} = \pi - 2\theta \)