When we do calculation for image location from spherical mirrors then normally we consider paraxial rays only, because paraxial rays
make calculations easier
are easier for geometrical analysis
contain most of the light intensity that is incident on mirror
can form point image for a point source
The correct Answer is:D
Defects like spherical aberrations are minimum for paraxial rays and thus these rays which are very close to principal axis are able to form sharp point images for point sources.
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - OBJECTIVE TYPE QUESTIONS (B. MULTIPLE CHOICE QUESTIONS)
21 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - OBJECTIVE TYPE QUESTIONS (JEE (MAIN) & OTHER STATE BOARDS FOR ENGINEERING ENTRANCE)
40 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - MODERN PUBLICATIONCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Revision Exercises (Numerical Problems)
36 Videos
- NUCLEIBOOK - MODERN PUBLICATIONCHAPTER - NUCLEIEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
15 Videos
- SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS BOOK - MODERN PUBLICATIONCHAPTER - SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS EXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
12 Videos
Similar Questions
Knowledge Check
Which of the following entities related to spherical mirrors do not depend on whether rays are paraxial or not ?
APoleBPrincipal axisCRadius of curvatureDfocal lengthWhich of the following entities related to spherical mirrors do not depend on whether rays are paraxial or not ?
ApoleBfocusCradius of curvatureDprincipal axisDuring the reflectio of ligth from plane mirror, the incident ray, normal and reflected ray lie
Aparalel to eacch otherBperpendicular to each otherCin same planeDin different plane
The inner surface of the wall of a sphere is perfectly reflecting. Radius of the sphere is R. A point source S is placed at a distance R/2 from the centre of the sphere. Consider the reflection of light from the farthest wall followed by reflection from the nearest wall. Where is the image of the source? Consider paraxial rays only.
View SolutionDo the laws of reflection change, when we use a spherical mirror instead of a plane mirror ?
View SolutionA point object (A) is kept at a distance (L) from a convex mirror on its principal axis. A glass slab is inserted between the object and the mirror with its refracting surfaces perpendicular to the principal axis of the mirror. The thickness of the slab is 6 cm and its refractive index is 32. The image formed after refraction through the slab, reflection from the mirror followed by refraction through the slab is a virtual image at a distance of 10 cm from the pole of the mirror (on its principal axis). Consider paraxial rays only and calculate the distance (L) of the object from the mirror. Focal length of the mirror is f=20cm.

View Solution
Rays parallel to principal axis, incident on the spherical mirror at different heights from principal axis are focused at different points. And due to this reason we cannot define unique focus. This is known as spherical aberration. Angle of incidence θ shown in figure depends on the height of ray above principal axis. Focal length of spherical mirror can be easily written in terms of angle θ shown in figure as follows :
f=R−R2secθ
Here R is radius of curvature of mirror. The light rays which are very close to principal axis are known as paraxial rays and rays far away from principal axis are called marginal rays.
Let fP and fm represent the focal length corresponding to paraxial rays and marginal rays respectively then
View Solution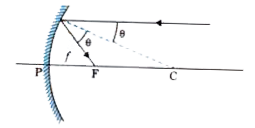
Rays parallel to principal axis, incident on the spherical mirror at different heights from principal axis are focused at different points. And due to this reason we cannot define unique focus. This is known as spherical aberration. Angle of incidence θ shown in figure depends on the height of ray above principal axis. Focal length of spherical mirror can be easily written in terms of angle θ shown in figure as follows :
f=R−R2secθ
Here R is radius of curvature of mirror. The light rays which are very close to principal axis are known as paraxial rays and rays far away from principal axis are called marginal rays.
For paraxial rays focal length is approximately
View Solution
