There is a sphere of radius R and refractive index μ. At what distance from the surface of sphere should an object be placed so that real image is formed at the same distance from the sphere ?
Rμ−1
Rμ
R2−μ
2Rμ−1
The correct Answer is:A
To solve the problem of finding the distance from the surface of a sphere at which an object should be placed to form a real image at the same distance from the sphere, we can follow these steps:
Step 1: Understand the Problem
We have a sphere with a radius R and a refractive index μ. We need to find the object distance u such that the real image is formed at the same distance v from the sphere.
Step 2: Set Up the Sign Convention
In optics, we typically use the following sign convention:
- Distances measured in the direction of the incident light (towards the surface) are considered negative.
- Distances measured in the direction of the outgoing light (away from the surface) are considered positive.
Step 3: Apply the Lens Maker's Formula
For a spherical surface, the lens maker's formula can be expressed as:
μ2v−μ1u=1R
Where:
- μ2 is the refractive index of the medium where the image is formed (for air, μ2=1).
- μ1 is the refractive index of the sphere (given as μ).
- R is the radius of the sphere.
Step 4: Substitute Values
Since we want the image to be formed at the same distance as the object, we can denote the distance from the surface of the sphere to the object as x. Therefore, we can write:
- u=−x (since it's measured towards the sphere)
- v=x (since it's measured away from the sphere)
Substituting these into the lens maker's formula gives:
1x−μ−x=1R
Step 5: Simplify the Equation
This simplifies to:
1x+μx=1R
Combining the fractions on the left side:
1+μx=1R
Step 6: Solve for x
Rearranging the equation to solve for x:
x=R(1+μ)
Step 7: Find the Distance from the Surface of the Sphere
Since x is the distance from the center of the sphere, the distance from the surface of the sphere is:
Distance from surface=x−R=R(1+μ)−R=Rμ
Final Answer
Thus, the object should be placed at a distance of Rμ from the surface of the sphere.
---
We have a sphere with a radius R and a refractive index μ. We need to find the object distance u such that the real image is formed at the same distance v from the sphere.
In optics, we typically use the following sign convention:
- Distances measured in the direction of the incident light (towards the surface) are considered negative.
- Distances measured in the direction of the outgoing light (away from the surface) are considered positive.
For a spherical surface, the lens maker's formula can be expressed as:
μ2v−μ1u=1R
Where:
- μ2 is the refractive index of the medium where the image is formed (for air, μ2=1).
- μ1 is the refractive index of the sphere (given as μ).
- R is the radius of the sphere.
Since we want the image to be formed at the same distance as the object, we can denote the distance from the surface of the sphere to the object as x. Therefore, we can write:
- u=−x (since it's measured towards the sphere)
- v=x (since it's measured away from the sphere)
1x−μ−x=1R
This simplifies to:
1x+μx=1R
Combining the fractions on the left side:
1+μx=1R
Rearranging the equation to solve for x:
x=R(1+μ)
Since x is the distance from the center of the sphere, the distance from the surface of the sphere is:
Distance from surface=x−R=R(1+μ)−R=Rμ
Thus, the object should be placed at a distance of Rμ from the surface of the sphere.
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBook:MODERN PUBLICATIONChapter:RAY OPTICS AND OPTICAL INSTRUMENTSExercise:OBJECTIVE TYPE QUESTIONS (B. MULTIPLE CHOICE QUESTIONS)
Explore 21 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBook:MODERN PUBLICATIONChapter:RAY OPTICS AND OPTICAL INSTRUMENTSExercise:OBJECTIVE TYPE QUESTIONS (JEE (MAIN) & OTHER STATE BOARDS FOR ENGINEERING ENTRANCE)
Explore 40 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBook:MODERN PUBLICATIONChapter:RAY OPTICS AND OPTICAL INSTRUMENTSExercise:Revision Exercises (Numerical Problems)
Explore 36 Videos
- NUCLEIBook:MODERN PUBLICATIONChapter:NUCLEIExercise:CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
Explore 15 Videos
- SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS Book:MODERN PUBLICATIONChapter:SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS Exercise:CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
Explore 12 Videos
Similar Questions
A sphere of radius R made of material of refractive index μ2 is placed in a medium of refractive index μ1. Where would an object be placed so that a real image is formed at equidistant fromk the sphere? ltbgt
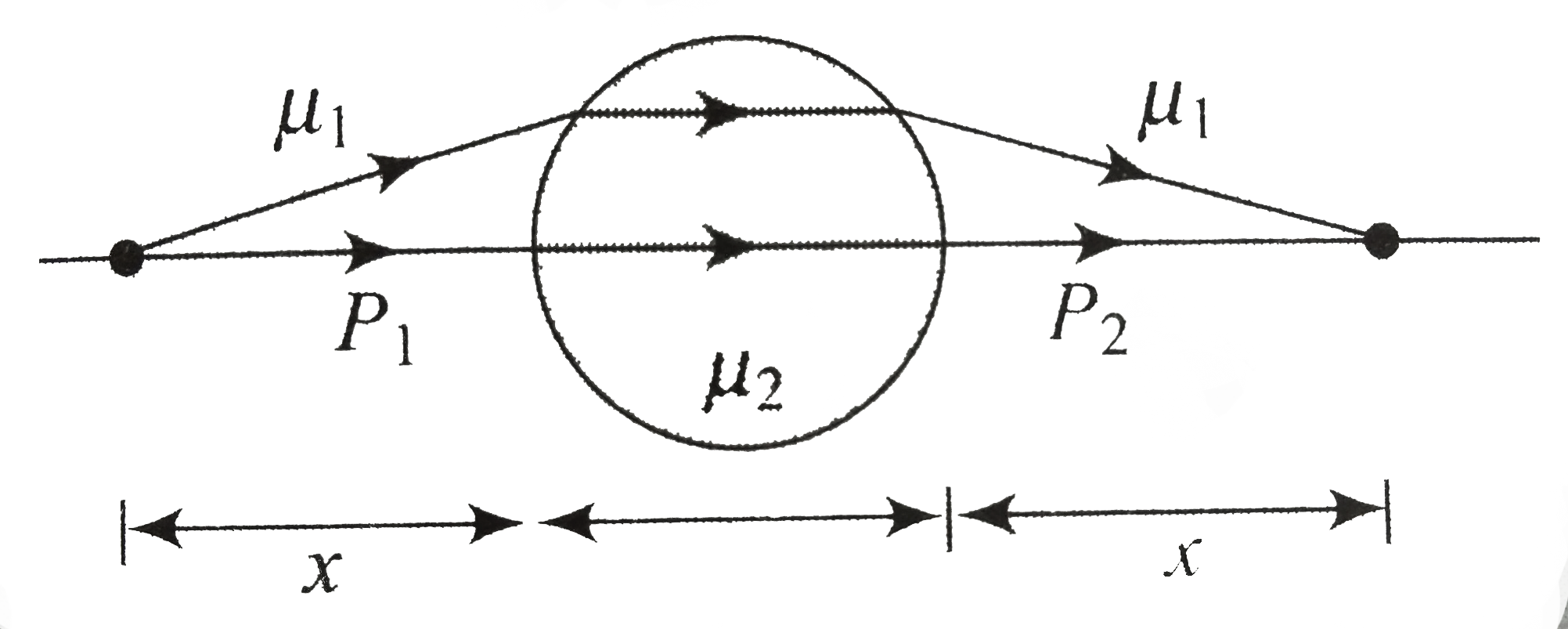
View SolutionA spherical surface of radius R ssparates two media of refractive indices μ1 and μ1 as shown in figure., Where should an object be placed in medium 1 so that a real image is formed in medium 2 at the same distance?
View Solution
Knowledge Check
A transparent sphere of radius R and refractie index μ is kept in air. At what distance from the surface of the sphere shold a point object be placed so as to form a rea image at the same distance from the sphere?
AR/μBμRCRμ−1DRμ+1The figure ,shows a transparent sphere of radiusRand refractive indexμ.An object Ois placed at a distance x from the pole of the first surface so that a real image is formed at the pole of the exactly opposite surface.
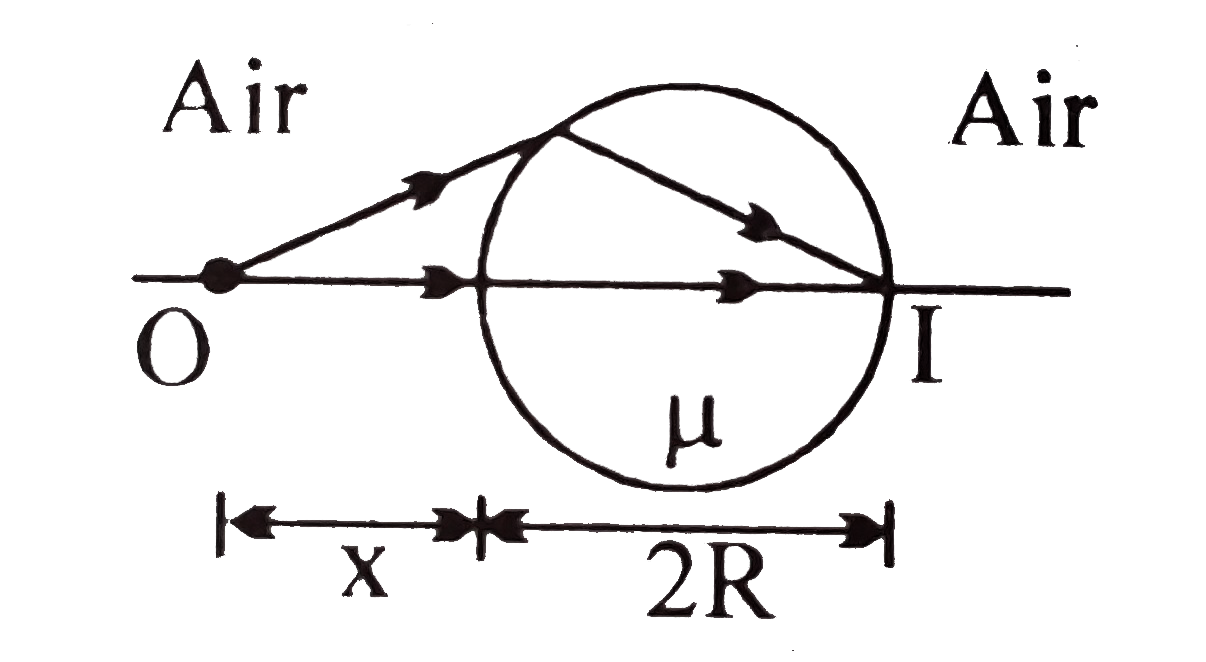 if an object is Placed at a distanceR from the pole of first surface ,then the real image is formed at a distance Rfrom thepole of the second surface.The refractive indexμ of the spher is given byA1.5B2C√2DNone of these
if an object is Placed at a distanceR from the pole of first surface ,then the real image is formed at a distance Rfrom thepole of the second surface.The refractive indexμ of the spher is given byA1.5B2C√2DNone of theseThe figure ,shows a transparent sphere of radiusRand refractive indexμ.An object Ois placed at a distance x from the pole of the first surface so that a real image is formed at the pole of the exactly opposite surface.
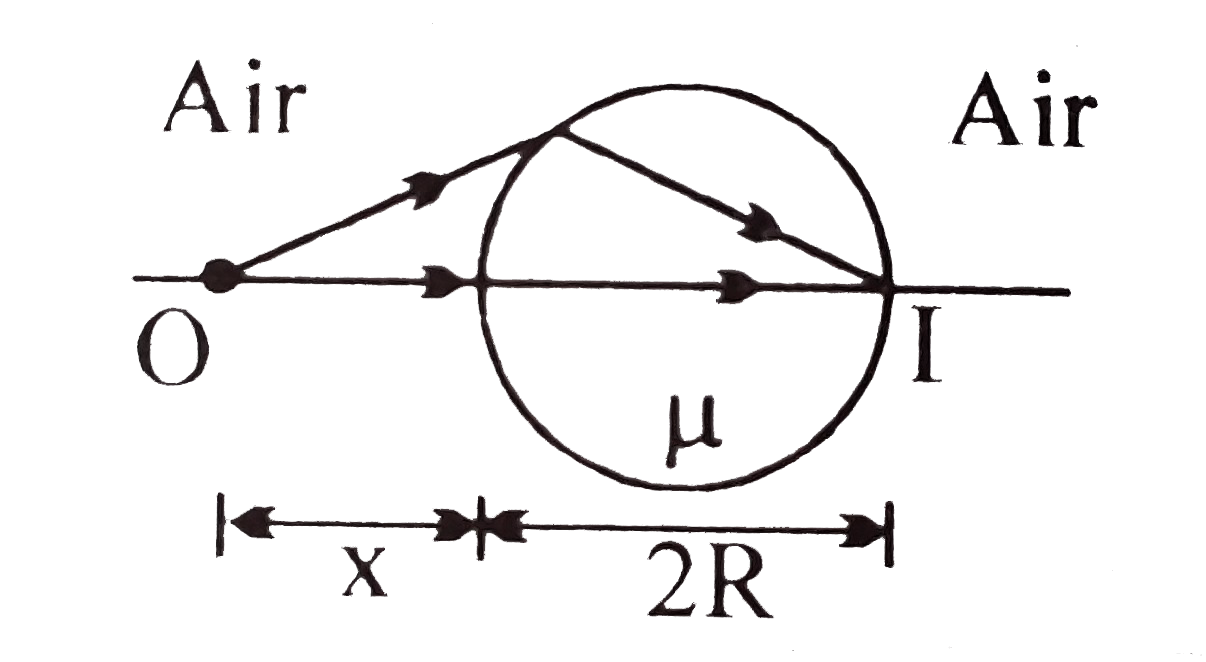
If x=2R,then the value of μisA1.5B2C3Dnone of these
An object is placed at a distance of 20 cm from a convex mirror of radius of curvature convex cm. At what distance from the object should a plane mirror be placed so that the images due to the mirror and the plane mirror are on the same plane?
View SolutionThe figure ,shows a transparent sphere of radiusRand refractive indexμ.An object Ois placed at a distance x from the pole of the first surface so that a real image is formed at the pole of the exactly opposite surface.
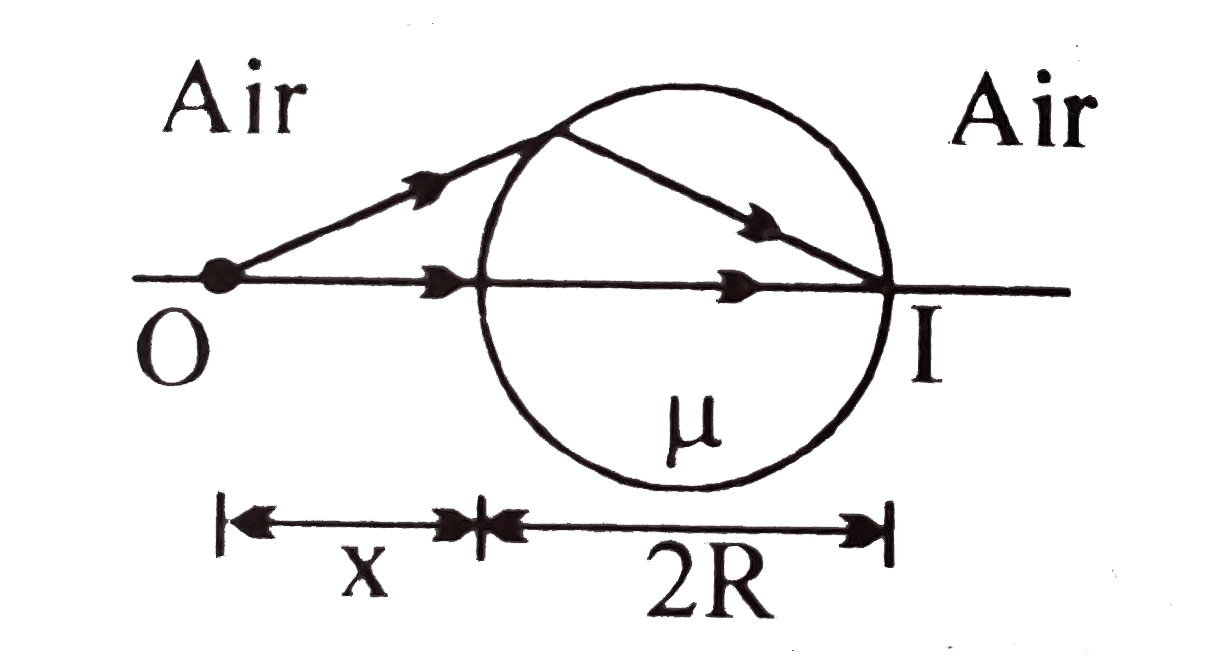 If x=∞,then the value of μ is
If x=∞,then the value of μ is
View SolutionAn air bubble is inside water. The refractive index of water is 4/3. At the what distance from the air bubble should a point object be placed so as to form a real image at the same distance from the bubble?
View SolutionAn air bubble inside water. The refractive index of water is 4/3 . At what distance from the air bubble should a point object be placed so as to form a real image at the same distance from the bubble:-
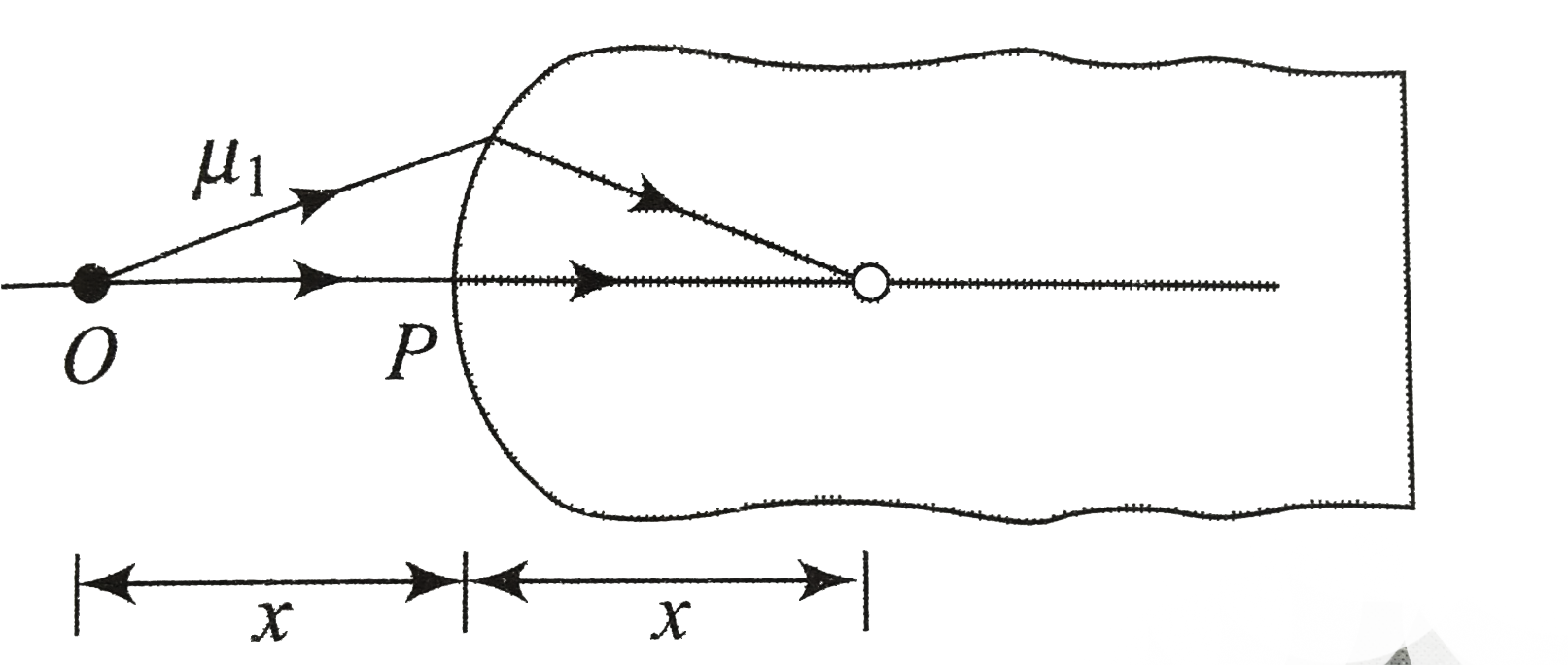
View SolutionA hemishperical surface of radius R and refractive index μ=1.5 is polished as shown. At what distance x from point P a point object O be placed so that its image coincides with the object itself?

View Solution

