A ray of light is incident on the surface of water. For what angle, the ray will undergo total internal reflection ?
To determine the angle at which a ray of light will undergo total internal reflection when it is incident on the surface of water, we need to understand the conditions required for total internal reflection (TIR) to occur.
1. Understanding Total Internal Reflection (TIR):
- Total internal reflection occurs when a light ray travels from a denser medium to a rarer medium and the angle of incidence exceeds a certain critical angle.
2. Identify the Media:
- In this scenario, we have water (denser medium) and air (rarer medium). The refractive index of water is approximately 1.33, and the refractive index of air is approximately 1.00.
3. Critical Angle Calculation:
- The critical angle (θ_c) can be calculated using Snell's Law, which states:
n1sin(θ1)=n2sin(θ2)
- For TIR, the angle of refraction (θ_2) is 90 degrees (since the light ray is refracted along the boundary), so:
nwatersin(θc)=nairsin(90∘)
- This simplifies to:
nwatersin(θc)=nair
- Plugging in the values:
1.33sin(θc)=1.00
4. Solving for the Critical Angle:
- Rearranging gives:
sin(θc)=1.001.33
- Now, calculating the value:
sin(θc)≈0.7519
- To find θ_c, take the inverse sine:
θc≈sin−1(0.7519)≈48.6∘
5. Conclusion:
- Therefore, the critical angle for total internal reflection when light travels from water to air is approximately 48.6 degrees. If the angle of incidence is greater than this critical angle, total internal reflection will occur.
Final Answer:
The ray will undergo total internal reflection at an angle greater than approximately 48.6 degrees.
---
- Total internal reflection occurs when a light ray travels from a denser medium to a rarer medium and the angle of incidence exceeds a certain critical angle.
- In this scenario, we have water (denser medium) and air (rarer medium). The refractive index of water is approximately 1.33, and the refractive index of air is approximately 1.00.
- The critical angle (θ_c) can be calculated using Snell's Law, which states:
n1sin(θ1)=n2sin(θ2)
- For TIR, the angle of refraction (θ_2) is 90 degrees (since the light ray is refracted along the boundary), so:
nwatersin(θc)=nairsin(90∘)
- This simplifies to:
nwatersin(θc)=nair
- Plugging in the values:
1.33sin(θc)=1.00
- Rearranging gives:
sin(θc)=1.001.33
- Now, calculating the value:
sin(θc)≈0.7519
- To find θ_c, take the inverse sine:
θc≈sin−1(0.7519)≈48.6∘
- Therefore, the critical angle for total internal reflection when light travels from water to air is approximately 48.6 degrees. If the angle of incidence is greater than this critical angle, total internal reflection will occur.
The ray will undergo total internal reflection at an angle greater than approximately 48.6 degrees.
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBook:MODERN PUBLICATIONChapter:RAY OPTICS AND OPTICAL INSTRUMENTSExercise:Tough & Tricky (PROBLEMS)
Explore 20 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBook:MODERN PUBLICATIONChapter:RAY OPTICS AND OPTICAL INSTRUMENTSExercise:NCERT FILE SOLVED (TEXT BOOK EXERCISES)
Explore 38 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBook:MODERN PUBLICATIONChapter:RAY OPTICS AND OPTICAL INSTRUMENTSExercise:PRACTICE PROBLEMS (11)
Explore 4 Videos
- NUCLEIBook:MODERN PUBLICATIONChapter:NUCLEIExercise:CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
Explore 15 Videos
- SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS Book:MODERN PUBLICATIONChapter:SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS Exercise:CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
Explore 12 Videos
Similar Questions
The path of a ray of light passing through an equilateral glass prism ABC is shown in figure. The ray of light is incident on face BC at the critical angle for just total internal reflection. The total internal reflection. The total angle of deviation after the refraction at face AC is 108∘. Calculate the refractive index of the glass.
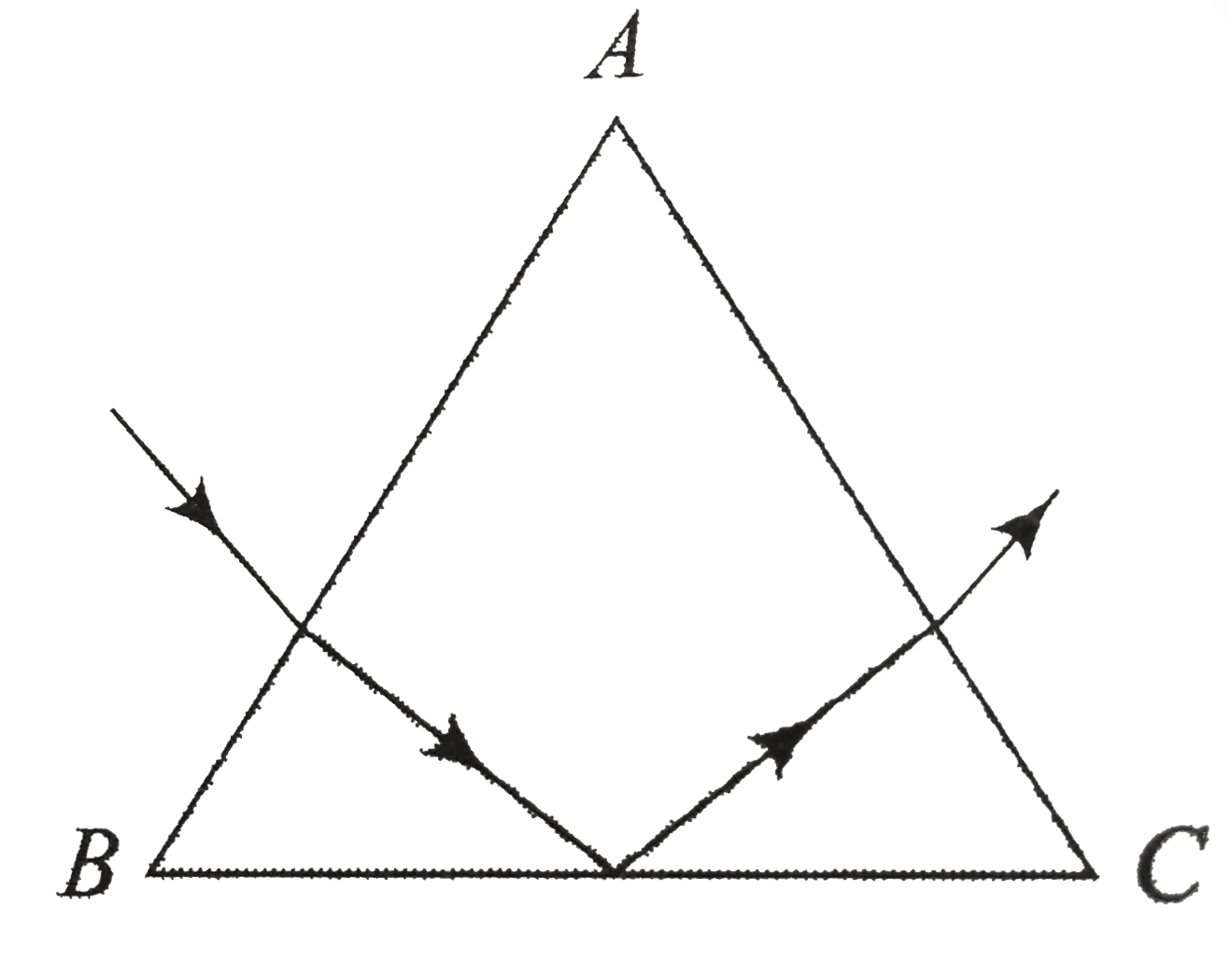
View SolutionShow that when a ray of light is incident on the surface of a transparent medium at the polarizing angle, the reflected ray and the refracted ray are at right angles to each other.
View Solution
Knowledge Check
A ray of light travelling in a transparent medium f refractive index μ, falls on a surface separating the medium from air at an angle of incidence of 45∘. For which of the following value of μ the ray can undergo total internal reflection ?
Aμ=1.33Bμ=1.40Cμ=1.50Dμ=1.25A ray of light travelling in transparent medium of refractive indexμfalls on a surface separating the medium from air at an angle of incidence of 45∘. For which of the following value of μthe ray can undergo total internal reflection ?
Aμ>1.33Bμ>1.4Cμ>1.5Dμ>1.25Two plane mirrror are inclined to each other at 70∘. A ray of light is incident on one mirror. They ray after two reflections will undergo a total deviation of :
A180∘B220∘C40∘DCannot be found because angle of incidence is not given
A ray of light is incident on the surface of a glass plate of reflective index 1.536 such that the reflected and refracted rays are mutually perpendicular. What is the angle of reflection ?
View SolutionShow that when a ray of light is incident on the surface of a transparent medilum at the polarising angle, the reflected and transmitted rays are perpendicular to each other.
View SolutionA ray of light is incident on the surface of a glass plate of refractive index 1.6 at polarzing angle. Calculate the angles of reflection and refraction.
View SolutionIf a ray of light incident on an opaque surface makes an angle of 30∘ with the mirror, what will be the angle of reflection of its corresponding reflected ray?
View SolutionA ray of light incident on a glass sphere (refractive index √3 ) suffers total internal reflection before emerging out exactly parallel to the incident ray. The angle of incidence was
View Solution

