A uniform charged disc whose total charge has magnitude q and whose radius is r rotates with constant angular velocity of magnitude ω. What is the magnetic dipole moment?
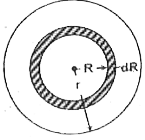
The surface charge density is q/πr2. Hence the charge within a ring of radius R and width dR is
dq=qπr2(2πRdR)=2qr3(RdR)
The current carried by this ring is its charge divided by the rotation period,
di=dq2π/ω=qωπr2[R.dR]
The magnetic moment contributed by this ring has the magnitude
dM = a |di|, where a is the area of ring.
dM=πR∘|di|=qωr2R3dR
M=∫dM=∫rR−0q.ωr2(R3dR)=qωr24
Topper's Solved these Questions
- MAGNETICBook:FIITJEEChapter:MAGNETICExercise:Solved Problems (Subjective)
Explore 10 Videos
- MAGNETICBook:FIITJEEChapter:MAGNETICExercise:Solved Problems (Objective)
Explore 14 Videos
- LAWS OF MOTIONBook:FIITJEEChapter:LAWS OF MOTIONExercise:COMPREHENSION-III
Explore 2 Videos
- MAGNETISMBook:FIITJEEChapter:MAGNETISMExercise:Example
Explore 12 Videos
Similar Questions
A uniformly charged thin conducting spherical shell of radius R and charge q is rotated with constant angular velocity ω about a diameter. The magnetic dipole moment of the system is
View SolutionA uniformly charged disc of radius r and having charge q rotates with constant angular velocity ω. The magnetic dipole moment of this disc is 1nqωr2. Find the value of n.
View Solution
Knowledge Check
A charge q is spread uniformly over an insulated loop of radius r. If it is rotated with an angular velocity ω with respect to normal axis then the magnetic moment of the loop is
A12qωr2B43qωr2C32qωr2Dqωr2A charge q is spread uniformly over an insulated loop of radius r. If it is rotated with an angular velocity ω with respect to normal axis then the magnetic moment of the loop is :
A43 qωr2B32 qωr2Cqωr2D12 qωr2A disc is rotating with angular velocity ω. If a child sits on it, what is conserved?
ALinear momentumBAngular momentumCkinetic energyDMoment of inertia
Charge Q is uniformly distributed over a nonconducting ring of radius R and mass m. It is made to rotate about an axis passing through its centre and perpendicular to its plone with an angular velocity of rotation ω. Find its magnetic dipole moment and its ratio with angular momentum.
View SolutionA rod has a total charge Q uniformly distributed along its length L. If the rod rotates with angular velocity ω about its end, compute its magnetic moment.

View SolutionSolid uniform conductiong sphere of mass 'm' and charge Q, rotates about its axis of symmetry with constant angular velocity 'ω' then the ratio of magnetic moment to the moment of inertia of the sphere is xQω6m then x is :(Neglect induced charges due to centrifugal force)
View SolutionAn electric dipole whose modulus is constant and whose moment is equal to p rotates with constant angular velocity ω about the axis draws at right angles to the axis of the dipole and passing through its midpoint. Find the power radiated by such a dipole.
View Solutionuniformly charged disc of radius R and total charge Q is rotating about its axis passing through the centre of diae and perpendicular to the plane of dise, with an angular velocity ω. Calculate its magnetic dipole moment. Also find the ratio of angular momentum to that with the calculated magnetic moment of the system.
View Solution

