A uniformly charged disc of radius r and having charge q rotates with constant angular velocity ω. The magnetic dipole moment of this disc is 1nqωr2. Find the value of n.
The correct Answer is:4
Step by step video, text & image solution for A uniformly charged disc of radius r and having charge q rotates with constant angular velocity omega. The magnetic dipole moment of this disc is (1)/(n)qomegar^(2). Find the value of n. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBook:DC PANDEYChapter:MAGNETIC EFFECT OF CURRENT AND MAGNETISMExercise:Matrix Matching type Questions
Explore 11 Videos
- LAWS OF THERMODYNAMICSBook:DC PANDEYChapter:LAWS OF THERMODYNAMICSExercise:Level 2 Subjective
Explore 18 Videos
- MEASUREMENT AND ERRORSBook:DC PANDEYChapter:MEASUREMENT AND ERRORSExercise:Subjective
Explore 19 Videos
Similar Questions
A uniformly charged thin conducting spherical shell of radius R and charge q is rotated with constant angular velocity ω about a diameter. The magnetic dipole moment of the system is
View SolutionA uniform charged disc whose total charge has magnitude q and whose radius is r rotates with constant angular velocity of magnitude ω. What is the magnetic dipole moment?
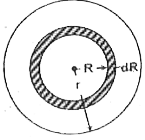
View Solution
Knowledge Check
An electron of chargee, revolves round in an orbit of radius r with a uniform angular velocity ω. The magnetic dipole moment of the electron in the orbit is
Aeωr/2Beωr2/2Ceω2r/2Deω2r2/2A non-conducting disc having unifrom positive charge Q, is rotating about its axis with unifrom angular velocity ω.The magnetic field at the centre of the disc is.
 Adirected outwardBhaving magnitude μ0Qω4πRCdirected inwardsDhaving magnitude μ0Qω2πR
Adirected outwardBhaving magnitude μ0Qω4πRCdirected inwardsDhaving magnitude μ0Qω2πRA thin disc of radius R and mass M has charge q uniformly distributed on it. It rotates with angular velocity ω. The ratio of magnetic moment and angular momentum for the disc is
Aq2MBR2MCq22MD2Mq
A conducting ring of radius r having charge q is rotating with angular velocity ω about its axes. Find the magnetic field at the centre of the ring.

View SolutionConsider a nonconductiing disc of radius r and mass m which has a charge q distributed uniformly over it. The disk is rotated about its axis with an angluar speed ω.Magnetic moment of the disc is 1Nqωr2.then find value of N.
View SolutionA ring of mass m and radius R is given a charge q. It is then rotated about its axis with angular velocity ω.Find
(iii)Magnetic moment of ring.
View SolutionA disc of radius R rotates with constant angular velocity ω about its own axis. Surface charge density of this disc varies as σ=αr2, where r is the distance from the centre of disc. Determine the magnetic field intensity at the centre of disc.
View SolutionA disc of mass m has a charge Q distributed on its surface. It is rotating about an XX' with a angular velocity ω. The force acting on the disc is

View Solution