Two block of mass m and M are connected means of a metal of a metal wire passing over a frictionless fixed pulley. The area of cross section of the wire is 6.67×10−9m2 and its breaking stress is 2×109Nm−2. If m = 1kg. Find the maximum value of M in kg for which the wire will not break. (g=10m/s2).
The correct Answer is:2
To solve the problem, we need to determine the maximum value of mass M such that the wire does not break when two blocks of mass m and M are connected over a frictionless pulley.
1. Understanding Breaking Stress:
The breaking stress of the wire is given as 2×109N/m2. Breaking stress is the maximum stress that the wire can withstand before breaking.
2. Calculating Maximum Tension:
The maximum tension Tmax in the wire can be calculated using the formula:
Tmax=Breaking Stress×Area of Cross Section
Given:
- Area of cross section A=6.67×10−9m2
- Breaking stress σ=2×109N/m2
Substituting the values:
Tmax=2×109N/m2×6.67×10−9m2=13.34N
3. Setting Up the Equations of Motion:
For the block of mass M:
Mg−T=Ma(1)
For the block of mass m (where m=1kg):
T−mg=ma(2)
Here, g=10m/s2.
4. Substituting Values in Equation (2):
Substituting m=1kg:
T−1⋅10=1⋅a
Simplifying:
T−10=a(3)
5. Substituting Equation (3) into Equation (1):
From equation (3), we can express a:
a=T−10
Substitute a in equation (1):
Mg−T=M(T−10)
Expanding:
Mg−T=MT−10M
Rearranging gives:
Mg+10M=T+MT
Factoring out T:
T(1+M)=Mg+10M
Thus:
T=Mg+10M1+M
6. Setting T to Maximum Tension:
We know T cannot exceed Tmax=13.34N:
Mg+10M1+M≤13.34
Substituting g=10:
M(10+10)1+M≤13.34
Simplifying:
20M1+M≤13.34
7. Cross Multiplying:
20M≤13.34(1+M)
Expanding:
20M≤13.34+13.34M
Rearranging gives:
20M−13.34M≤13.34
6.66M≤13.34
Thus:
M≤13.346.66≈2kg
Conclusion:
The maximum value of M for which the wire will not break is approximately 2kg.
The breaking stress of the wire is given as 2×109N/m2. Breaking stress is the maximum stress that the wire can withstand before breaking.
The maximum tension Tmax in the wire can be calculated using the formula:
Tmax=Breaking Stress×Area of Cross Section
Given:
- Area of cross section A=6.67×10−9m2
- Breaking stress σ=2×109N/m2
Tmax=2×109N/m2×6.67×10−9m2=13.34N
For the block of mass M:
Mg−T=Ma(1)
For the block of mass m (where m=1kg):
T−mg=ma(2)
Here, g=10m/s2.
Substituting m=1kg:
T−1⋅10=1⋅a
Simplifying:
T−10=a(3)
From equation (3), we can express a:
a=T−10
Substitute a in equation (1):
Mg−T=M(T−10)
Expanding:
Mg−T=MT−10M
Rearranging gives:
Mg+10M=T+MT
Factoring out T:
T(1+M)=Mg+10M
Thus:
T=Mg+10M1+M
We know T cannot exceed Tmax=13.34N:
Mg+10M1+M≤13.34
Substituting g=10:
M(10+10)1+M≤13.34
Simplifying:
20M1+M≤13.34
20M≤13.34(1+M)
Expanding:
20M≤13.34+13.34M
Rearranging gives:
20M−13.34M≤13.34
6.66M≤13.34
Thus:
M≤13.346.66≈2kg
The maximum value of M for which the wire will not break is approximately 2kg.
Topper's Solved these Questions
- LAWS OF MOTIONBook:FIITJEEChapter:LAWS OF MOTIONExercise:MATRIX MATCH TYPE
Explore 4 Videos
- LAWS OF MOTIONBook:FIITJEEChapter:LAWS OF MOTIONExercise:Exercise
Explore 15 Videos
- LAWS OF MOTIONBook:FIITJEEChapter:LAWS OF MOTIONExercise:ASSERTION REASONING TYPE
Explore 1 Video
- KINEMATICSBook:FIITJEEChapter:KINEMATICSExercise:NUMERICAL BASED QUESTIONS DECIMAL TYPE
Explore 5 Videos
- MAGNETICBook:FIITJEEChapter:MAGNETICExercise:Numerical Based Type
Explore 2 Videos
Similar Questions
Two blocks of masses m and M are connected by means of a metal wire passing over a frictionless fixed pulley. The area of cross-section of the wire is 6.5×10−9m2 and its breaking stress is 2×109Nm−2. If m = 1kg, then calculate the maximum value of M (g=10m/s2)
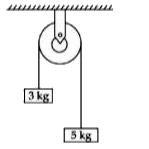
View SolutionTwo blocks of masses 3 kg and 5 kg are connected by a metal wire going over a smooth pulley. The breaking stress of the metal is 24π×102Nm−2 . What is the minimum radius of the wire ?
(take g=10ms−2)
View Solution
Knowledge Check
Two blocks of masses m and 2m are connected through a wire fo breakig stress S passing over a frictionless pulley. The maximum radius of the wire to be used so that the wire may not break is
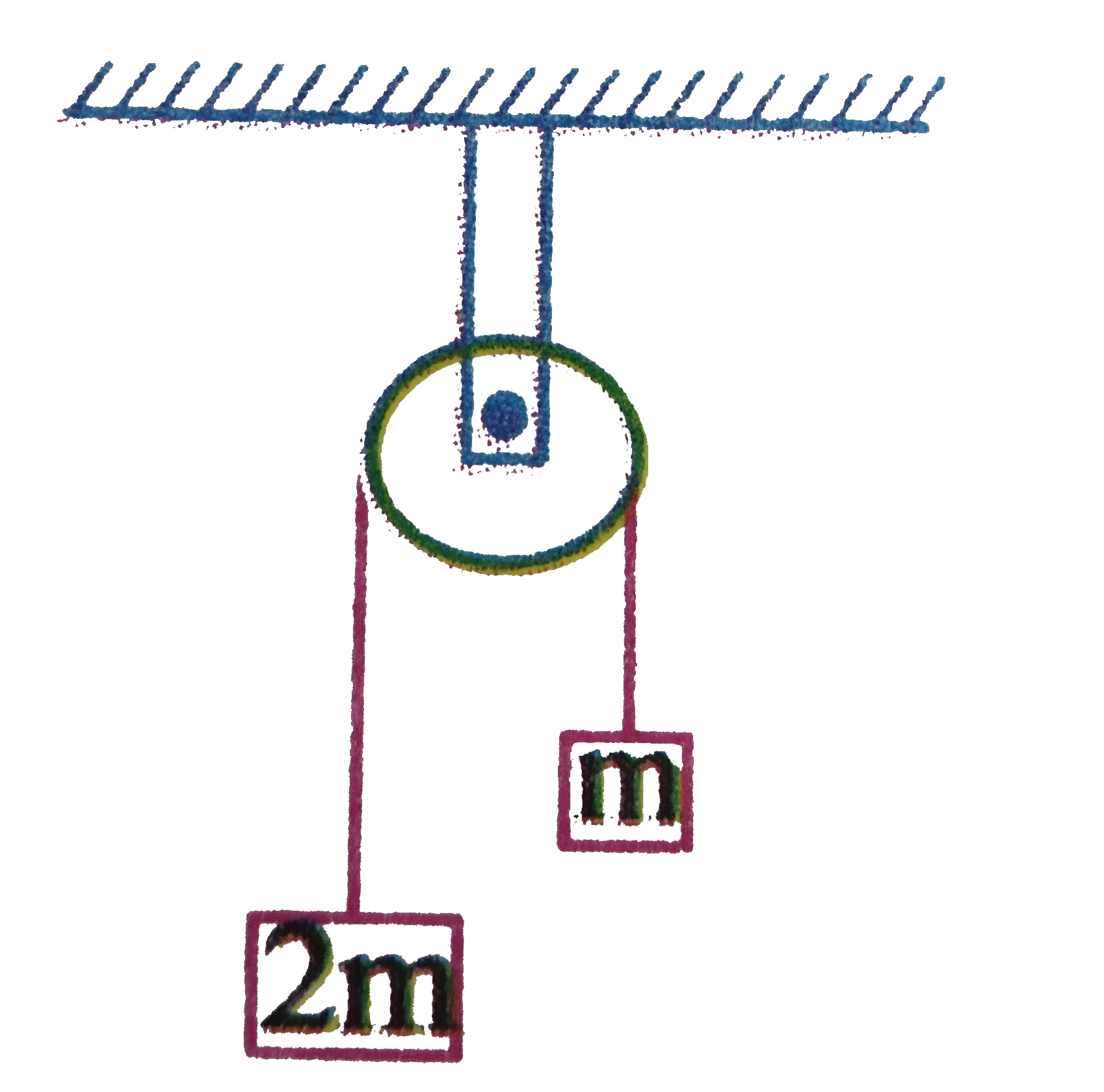 A√34mgπSB√43mgSC√433gπSD√12mgπS
A√34mgπSB√43mgSC√433gπSD√12mgπSTwo blocks of masses m1=4kg and m2=2kg are connected to the ends of a string which passes over a massless, frictionless pulley. The total downwards thrust on the pulley is nearly
 A27 NB54 NC0.8 NDZero
A27 NB54 NC0.8 NDZeroTwo blocks of masses 5 kg and 10 kg are connected by a metal wire going over a smooth pulley as shown in the figure. The breaking stress of the metal wire is 2×109N m−2. If g=10ms−2, then what is the minimum radius of the wire which will not break
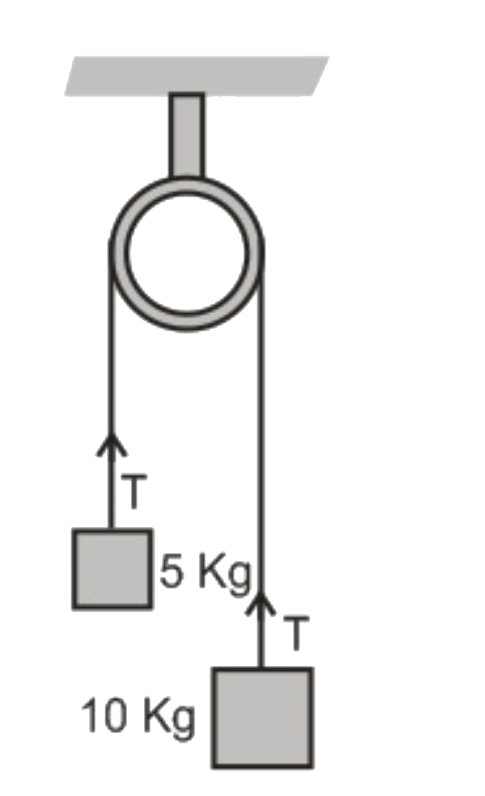 A0.1 mmB0.2 mmC0.05 mmD0.25 mm
A0.1 mmB0.2 mmC0.05 mmD0.25 mm
A wire of length 1m is stretched by a force of 10N. The area of cross-section of the wire is 2×10–6m2 and Y is 2×1011N/m2 . Increase in length of the wire will be -
View SolutionThe breaking stress of a wire is 7.2×108N/m2 and density is 78×102kg/m3. The wire is held vertically to the rigid support. The maximum length so that the wire does not break is
View SolutionTwo blocks of masses 1kg and 2kg are connected by a metal wire goijng over a smooth pulley as shown in figure.
The breaking stress of the metal is (40/3π)×106N/m2. If g=10ms−12, then what should be the minimum radlus of the wire used if it is not to break?

View SolutionFor steel the breaking stressis 6×106N/m2 and the density is 8×103kg/m3. The maximum length of steel wire, which can be suspended witout breaking under its own weight is [g=10m/s2]
View SolutionThe resistivity of a potentiometer wire is 40×10−8Ω−m and its area of cross section is 8×10−6m2. If 0.2 A current is flowing through the wire the potential gradient will be
View Solution

