A massive platform of mass M is moving with speed v=6ms−1 At t = 0, at body of mass m(m<<M) is gently placed on the platform. If c-efficient of friction between the body and platform is μ=0.3andg=10m/s2, then
the body covers a distance of 3 m on the platform in the direction of motion of the platform.
the body covers a distance of 3 m on the platform opposite to the direction of motion of the platform before coming to rest.
the body covers a distance of 6 m on the platform in the direction of motion of the platform.
the body covers a distance of 6 m on the platform opposite to the direction of motion of the platform before coming to rest.
The correct Answer is:D
To solve the problem, we need to analyze the motion of the body of mass m placed on the moving platform of mass M. The platform is moving with a speed v=6m/s, and the coefficient of friction between the body and the platform is μ=0.3. The acceleration due to gravity is g=10m/s2.
1. Identify Initial Conditions:
- The platform is moving with a speed v=6m/s.
- The body of mass m is placed gently on the platform, which means its initial relative velocity with respect to the platform is 0m/s.
2. Determine Relative Velocity:
- The initial velocity of the body m with respect to the ground is 6m/s (same as the platform).
- When the body is placed on the platform, it starts with an initial velocity of 0 relative to the platform. Thus, the relative velocity of the body with respect to the platform is:
v21=v2−v1=0−6=−6m/s
- This indicates that the body is moving leftward with respect to the platform.
3. Friction Force:
- The friction force Fk acting on the body is given by:
Fk=μ⋅N
- The normal force N acting on the body is equal to its weight, which is:
N=m⋅g
- Therefore, the frictional force becomes:
Fk=μ⋅m⋅g=0.3⋅m⋅10=3mN
- This frictional force acts in the rightward direction (opposite to the leftward relative motion).
4. Calculate Acceleration:
- According to Newton's second law, the acceleration a of the body can be calculated as:
Fk=m⋅a⟹3m=m⋅a⟹a=3m/s2
- The acceleration is positive, indicating that it acts in the rightward direction.
5. Use the Equation of Motion:
- We need to find the distance x covered by the body before it comes to rest. The final velocity v=0 when the body stops.
- Using the equation of motion:
v2=u2+2ax
- Here, u=−6m/s (initial velocity), v=0, and a=3m/s2:
0=(−6)2+2⋅(−3)⋅x
0=36−6x
6x=36⟹x=6m
6. Conclusion:
- The body covers a distance of 6m on the platform before coming to rest.
Final Answer:
The body covers a distance of 6m on the platform opposite to the direction of motion of the platform before coming to rest.
---
- The platform is moving with a speed v=6m/s.
- The body of mass m is placed gently on the platform, which means its initial relative velocity with respect to the platform is 0m/s.
- The initial velocity of the body m with respect to the ground is 6m/s (same as the platform).
- When the body is placed on the platform, it starts with an initial velocity of 0 relative to the platform. Thus, the relative velocity of the body with respect to the platform is:
v21=v2−v1=0−6=−6m/s
- This indicates that the body is moving leftward with respect to the platform.
- The friction force Fk acting on the body is given by:
Fk=μ⋅N
- The normal force N acting on the body is equal to its weight, which is:
N=m⋅g
- Therefore, the frictional force becomes:
Fk=μ⋅m⋅g=0.3⋅m⋅10=3mN
- This frictional force acts in the rightward direction (opposite to the leftward relative motion).
- According to Newton's second law, the acceleration a of the body can be calculated as:
Fk=m⋅a⟹3m=m⋅a⟹a=3m/s2
- The acceleration is positive, indicating that it acts in the rightward direction.
- We need to find the distance x covered by the body before it comes to rest. The final velocity v=0 when the body stops.
- Using the equation of motion:
v2=u2+2ax
- Here, u=−6m/s (initial velocity), v=0, and a=3m/s2:
0=(−6)2+2⋅(−3)⋅x
0=36−6x
6x=36⟹x=6m
- The body covers a distance of 6m on the platform before coming to rest.
The body covers a distance of 6m on the platform opposite to the direction of motion of the platform before coming to rest.
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - FIITJEECHAPTER - LAWS OF MOTIONEXERCISE - COMPREHENSION - I
6 Videos
- LAWS OF MOTIONBOOK - FIITJEECHAPTER - LAWS OF MOTIONEXERCISE - COMPREHENSION - II
5 Videos
- LAWS OF MOTIONBOOK - FIITJEECHAPTER - LAWS OF MOTIONEXERCISE - SOLVED PROBLEMS (SUBJECTIVE)
11 Videos
- KINEMATICSBOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - NUMERICAL BASED QUESTIONS DECIMAL TYPE
5 Videos
- MAGNETICBOOK - FIITJEECHAPTER - MAGNETICEXERCISE - Numerical Based Type
2 Videos
Similar Questions
A particle of mass m connected with a hanging bob of mass M by an inextensible string is stationary relative to the rotating platform . The coefficient of static friction between the particle and platform is μ

Find the
a. maximum angular speed ω1
b. maximum angular speed ω2
(forM>μm)
View SolutionA rod AB of length 2m is hinging at point A and its other end B is attached to a platform on which a point of mass m is kept. Rod rotates about point A maintain angle θ=30∘ with the vertical in such a way that platform remain horizontal and revolves on the horizontal circular path. If the coefficient of static friction between the block and platform is μ=0.1 then find the maximum angular velocity in rads−1 of rod so that the block does not slip on the platform (g=10ms−2)
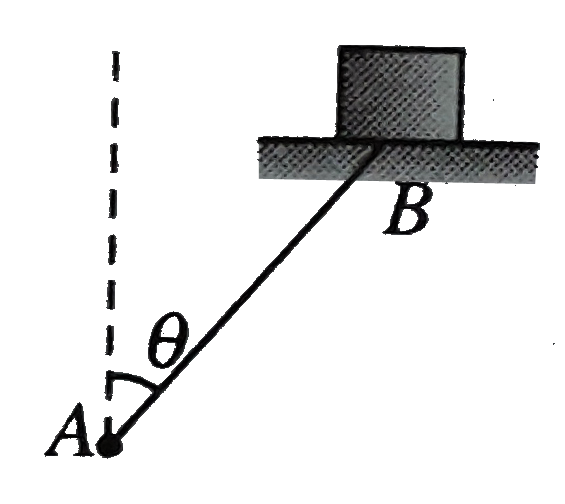
View Solution
Knowledge Check

In the given figure, a long platform of mass m is placed on frictionless surface. Two blocks of masses 4 m and m (where m=10 kg) are placed on the platform. For both blocks, the coefficient of static friction with platform equal to 0.16 and the coefficient of kinetic friction equal to 0.10 the blocks are connected by a light ideal string through a light pulley (mounted at a movable massless stand). Which is acted upon by an unknown horizontal force F. if the acceleration of the platform is 2m/s2. Find the value of unknown force F and acceleration of blocks 4 m and m on a1 and a2 respectively.AF(N)a1(m/s2)a2(m/s2)180N2m/s28m/s2BF(N)a1(m/s2)a2(m/s2)180N8m/s22m/s2CF(N)a1(m/s2)a2(m/s2)90N2m/s28m/s2DF(N)a1(m/s2)a2(m/s2)90N8m/s22m/s2A body of mass m moving with a velocity v strikes a statioinalry body of mass m and sticks to it. What is the speed of the system?
A2vBvCv2Dv3A solid block of mass m=1kg is reasting on a horizontal platform as shown in figure. The z direction is vertically up. Coefficient of friction between the block and the paltform is μ=0.2. The platform is moved with a time dependent velocity given →V=(2tˆi+tˆj+3ˆk)m/s. Then the magnitude of the net force exerted by the block on the platform is : (Take g=10m/s2)
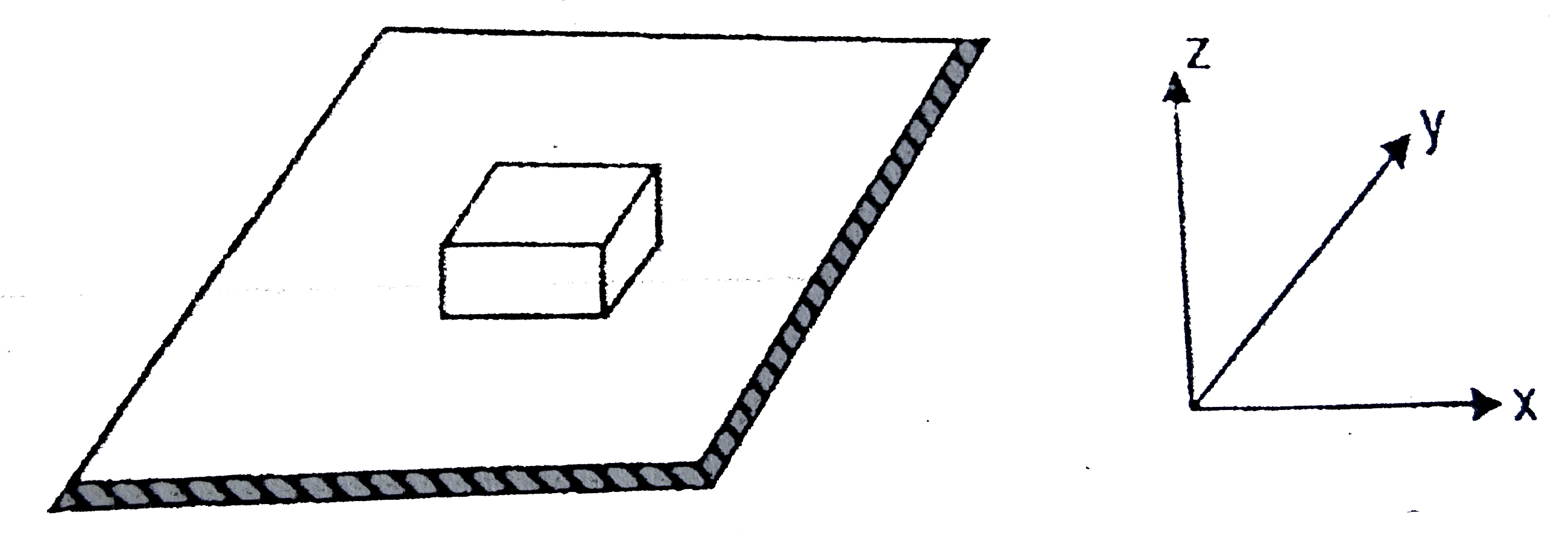 A√168NB√174NC√194NDNone of these
A√168NB√174NC√194NDNone of these
A solid block of mass m = 1 kg is resting on a horizontal platform as shown in figure. The z direction is vertically up. Coefficient of friction between the block and the platform is μ=0.2. The platform is moved with a time dependent velocity givenby →V=(2tˆi+tˆj+3tˆk)m/s . Calculate the magnitude of the force exerted by the block on the platform. Take g=10m/s2

View SolutionA platform of infinite mass is moving upward with velocity 5m/s. At time t=0, a ball which is at height 100m above the platform starts fallng freely. If the velocity of ball just after the collision is 10vm/s then value of v is (Assum elastic collision) (g=10m/s2):
View SolutionA skater of mass m standing on ice throws a stone of mass M =2m with a velocity of v=5m/s in horizontal direction. If the coefficient of friction between the skater and the ice is 0.5 , find the distance over which the skater will move ( take g=10ms−2)
View SolutionA horizontal platform is undergoing vertical S.H>M of time period T. A block of mass M is placed on the platform . The maximum mplitude of the platform so that the block is not detached form it is
View SolutionTwo block of masses m1 and m2 are connected with a massless unstretched spring and placed over a plank moving with an acceleration 'a' as shown in figure. The coefficient of friction between the blocks and platform is μ
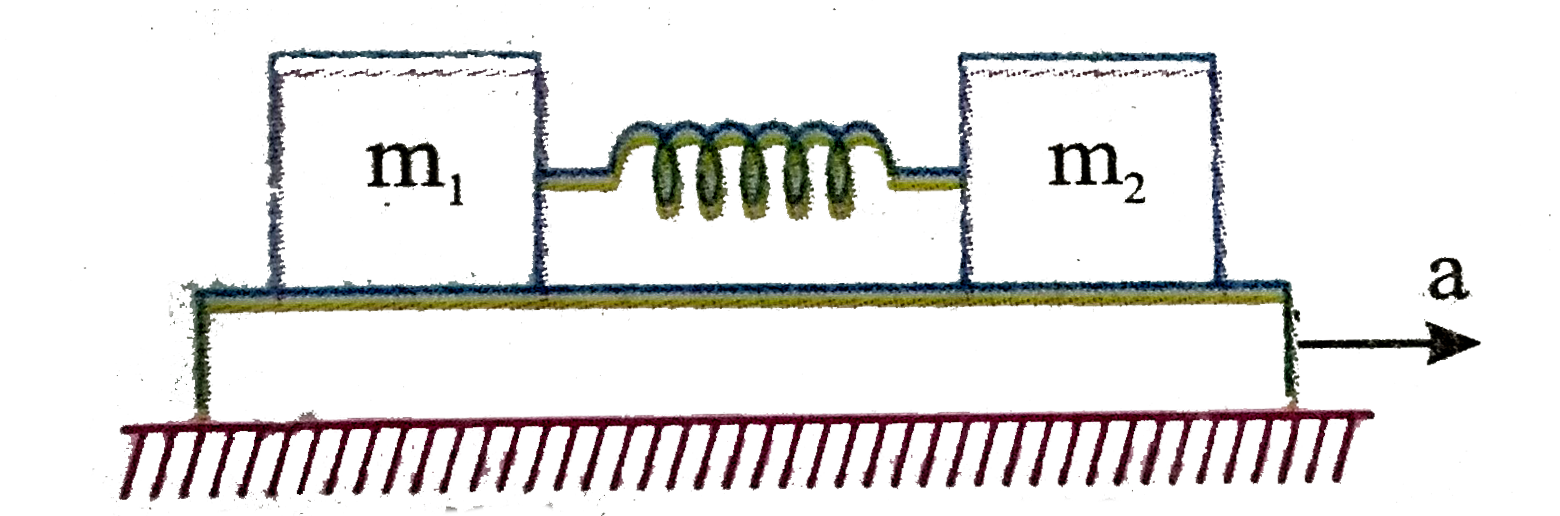
View Solution
