In the given figure, the wedge is acted upon by a constant horizontal force F. The wedge is moving on a smooth horizontal surface. A ball of mass 'm' is at rest relative to the wedge. The ratio of forces exerted on 'm' by the wedge when F is acting, and when F is withdrawn, assuming no friction between the wedge and the ball, the ratio is equal to

sec2θ
cos2θ
1
none of these.
The correct Answer is:A
The ball moves along x-axis with an acceleration, say a, whereas it is in equilibrium along y axis
⇒ΣFx=0⇒Rsinθ=ma
and ΣFy=0⇒Rcosθ=mg
⇒R=mgsecθ ...(1)
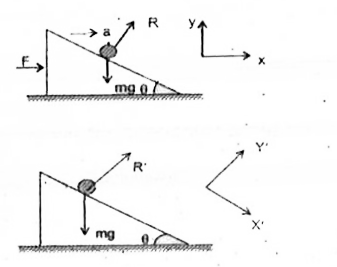
When F−0, Next the ball moves down the plane, along X axis, say with an acceleration a.
⇒mgsinθ=ma.
The ball does not move perpendicular to the plane. It is in equilibriumalong y - axis
⇒mgcosθ−R.=0
⇒R.=mgcosθ ...(2)
Dividing (1) by (2) ⇒RR.=sec2θ
Topper's Solved these Questions
- LAWS OF MOTIONBook:FIITJEEChapter:LAWS OF MOTIONExercise:COMPREHENSION - I
Explore 6 Videos
- LAWS OF MOTIONBook:FIITJEEChapter:LAWS OF MOTIONExercise:COMPREHENSION - II
Explore 5 Videos
- LAWS OF MOTIONBook:FIITJEEChapter:LAWS OF MOTIONExercise:SOLVED PROBLEMS (SUBJECTIVE)
Explore 11 Videos
- KINEMATICSBook:FIITJEEChapter:KINEMATICSExercise:NUMERICAL BASED QUESTIONS DECIMAL TYPE
Explore 5 Videos
- MAGNETICBook:FIITJEEChapter:MAGNETICExercise:Numerical Based Type
Explore 2 Videos
Similar Questions
In the given the wedge is acted upon by a constant horizontal force 'F'. The wedge is moving on a smooth horizontal surface A ball of mas 'm' is at rest relative to the wedge The ratio of forces exerted on 'm' by the wedge when 'F' is acting and 'F' is withdrawn assuming no friction between the edge and the ball is equal to .
View SolutionA block of mass m is at rest on a rought wedge as shown in figure. What is the force exerted by the wedge on the block?

View Solution
Knowledge Check
Block of mass m is stationary w.r.t. wedge. Normal force exerted by wedge on the block is
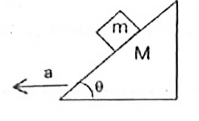 AmgcosθBmgcosθCmgsinθDmgsinθ
AmgcosθBmgcosθCmgsinθDmgsinθAll the surfaces are smooth as shown in figure. The acceleration of mass m relative to wedge is :
 Ag sin θBg sin θ + a cos θCg sin θ - a cos θDa cos θ
Ag sin θBg sin θ + a cos θCg sin θ - a cos θDa cos θa Block of mass m is placed on a wedge of mass M there is no friction between the block and the wedge .The minmum coefficient of friction between the wedge and the gound so that wedge does not move is,
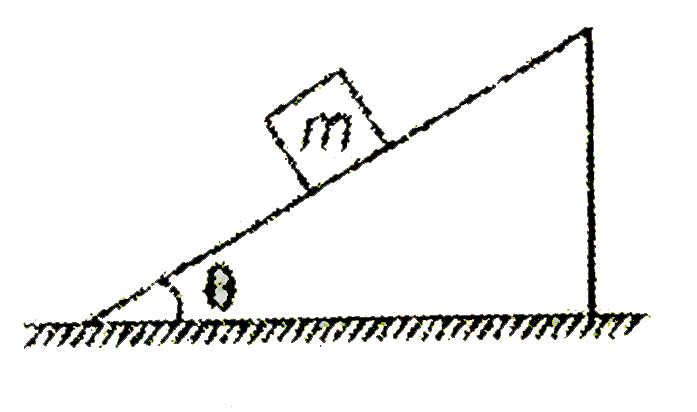 Amcos2θM+mcos2θBmsin2θM+mcos2θCmcosθsinθM+mcos2θDmcosθsinθM+msin2θ
Amcos2θM+mcos2θBmsin2θM+mcos2θCmcosθsinθM+mcos2θDmcosθsinθM+msin2θ
A wedge of mass M makes an angle θ with the horizontal. The wedge is placed on horizontal frictionless surface. A small block of mass m is placed on the inclined surface of wedge. What horizontal force F must be applied to the wedge so that the force of friction between the block and wedge is zero ?
View SolutionA block of mass m is placed at rest on a smooth wedge of mass M placed at rest on a smooth horizontal surface. As the system is released

View SolutionA small ball ( uniform solid sphere ) of mass m is released from the top of a wedge of the same mass m. The wedge is free to move on a smooth horizontal surface. The ball rolld without sliding on the wedge. The required height of the wedge are mentioned in the figure.
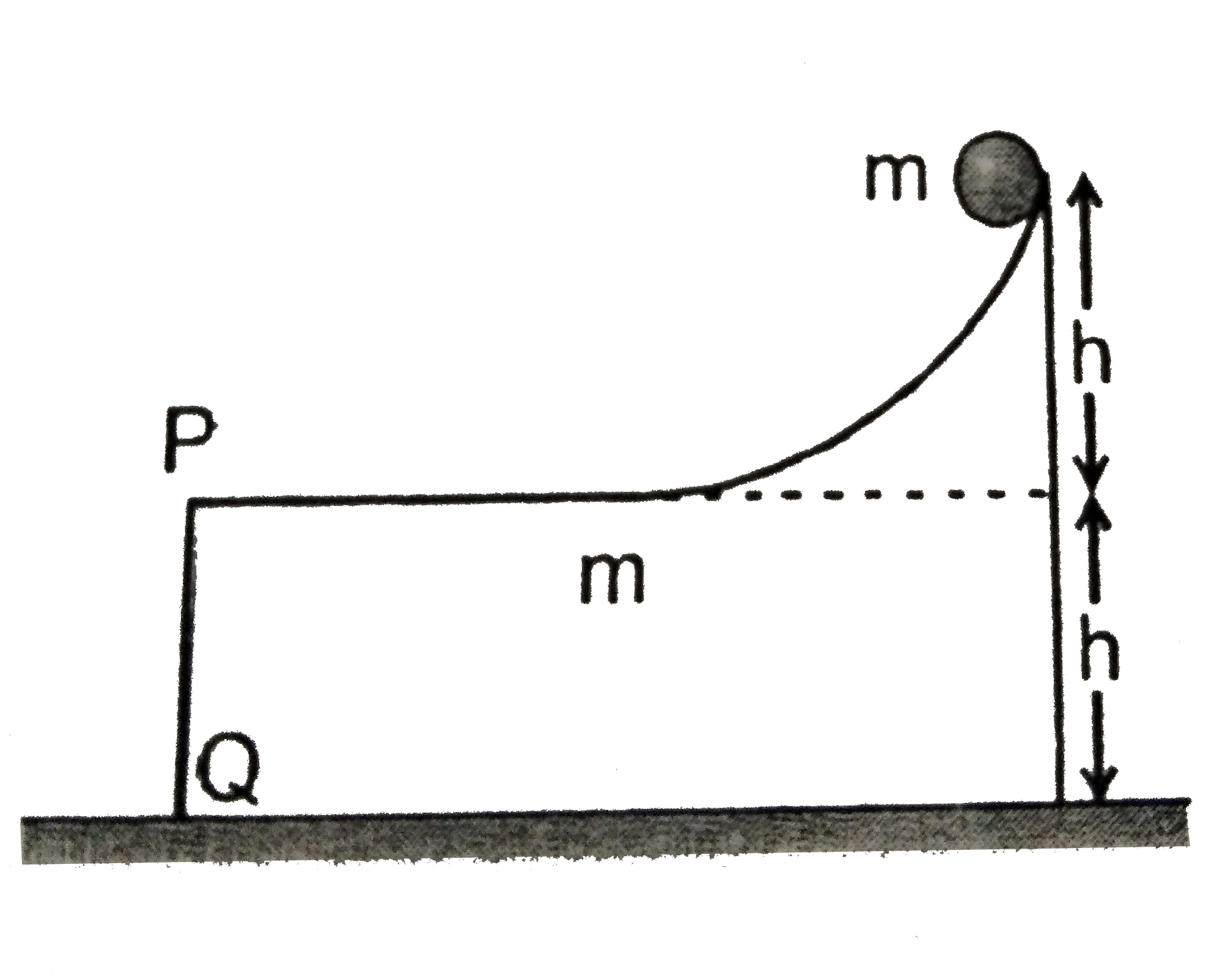
The speed of the wedge when the ball is just going to leave the wedge at point 'P' of the wedge is
View SolutionAs shown in the figure, a wedge of mass M is placed on a smooth inclined ramp that makes an angle θ to the horizontal. An object of mass m rests on top of the wedge. The sliding down the ramp at acceleration a. determine the apparent weight of the objects as it slides down. noth that there is friction between the object and the wedge so that the object remains relatively at rest on the wedge.

View SolutionA small ball ( uniform solid sphere ) of mass m is released from the top of a wedge of the same mass m. The wedge is free to move on a smooth horizontal surface. The ball rolld without sliding on the wedge. The required height of the wedge are mentioned in the figure.

The horizontal separation between the ball and the edge 'PQ' of wedge just before the ball falls on the groun is
View Solution

