A particle of mass m connected with a hanging bob of mass M by an inextensible string is stationary relative to the rotating platform . The coefficient of static friction between the particle and platform is μ

Find the
a. maximum angular speed ω1
b. maximum angular speed ω2
(forM>μm)
T=Mg
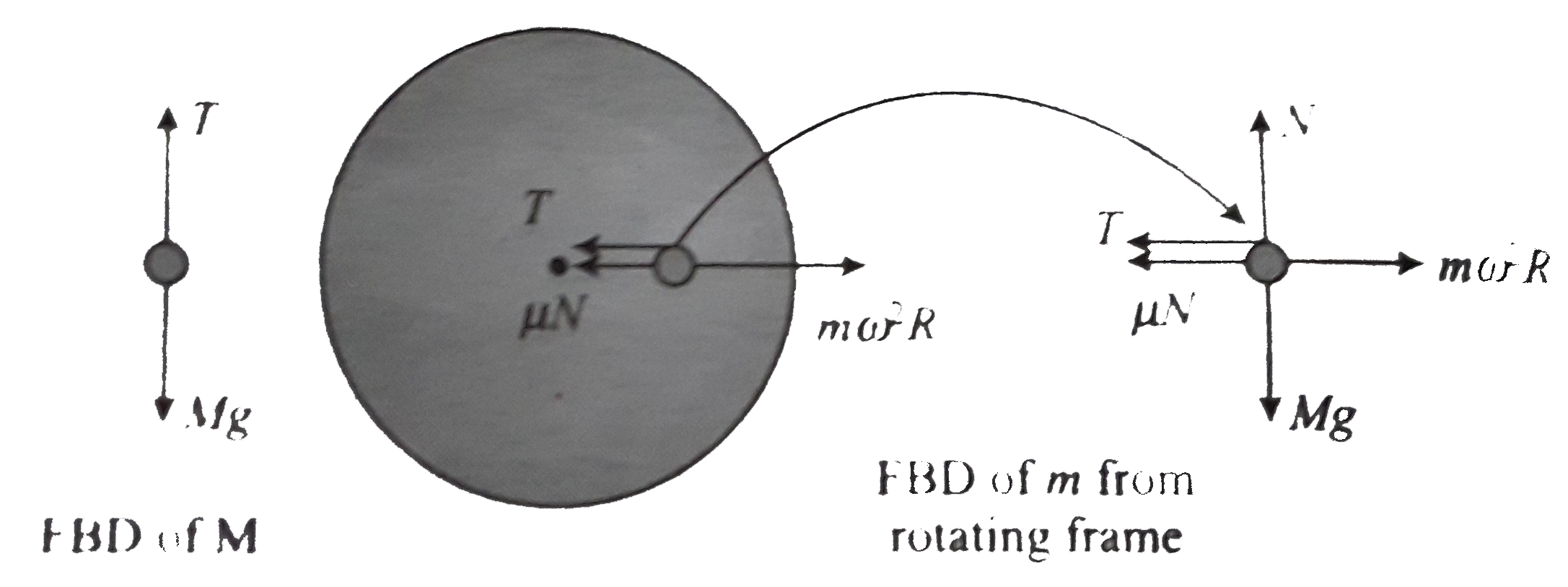
T+μN=mω2R
Mg+μMg=mω2R
ωmax=√(M+μm)gmR
For maximum angular velocity , the direction of friction will be toward radius direction (away from center) Hence.
ωmin=√(M+μm)gmR
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Solved Examples
12 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Exercise 7.1
25 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer
5 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
A car has to move on a level turn of radius 45 m. If the coefficient of static friction between the tire and the road is μs=2.0, find the maximum speed the car can take without skidding.
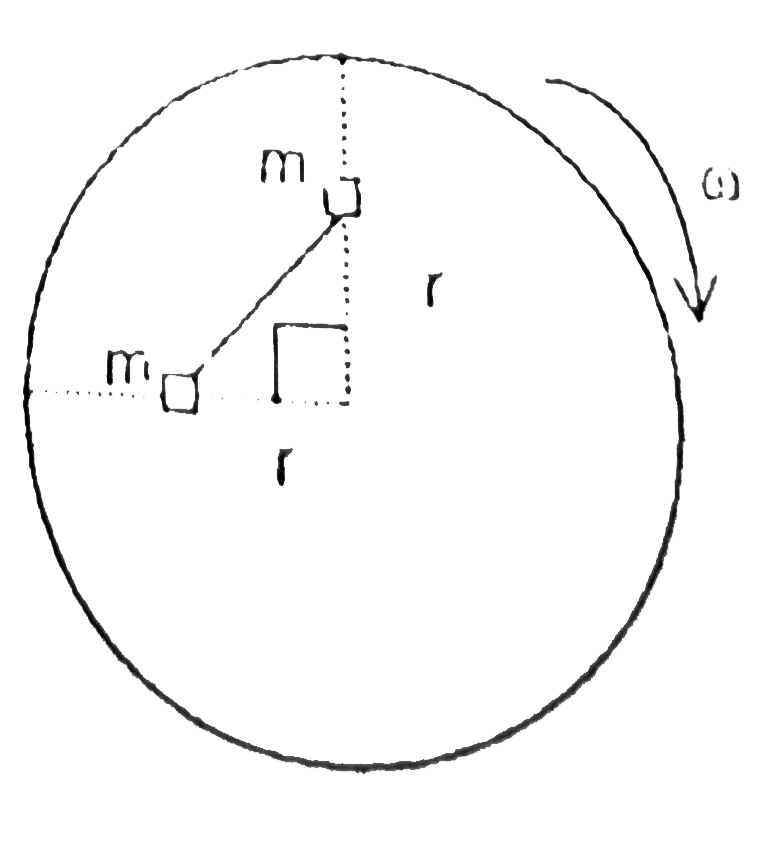
View SolutionTwo particles of mass m each are kept on a horizontal circular platfrom on two mutually perpendicular radii at equal distance r from the center of the table. The particles are connected with a string, which is just taught when the platfrom is not rotating. The coefficient of static friction between the platfrom and block is μ (now if angular speed of platfrom m is slowly increased). Find the maximum angular speed (ω) of platfrom about it center so that the blocks remain stationery relative to platform. (If μ=1√2, r=2.5m and g=10m/s2)
View Solution
Knowledge Check
Two block of masses m1 and m2 are connected with a massless unstretched spring and placed over a plank moving with an acceleration 'a' as shown in figure. The coefficient of friction between the blocks and platform is μ
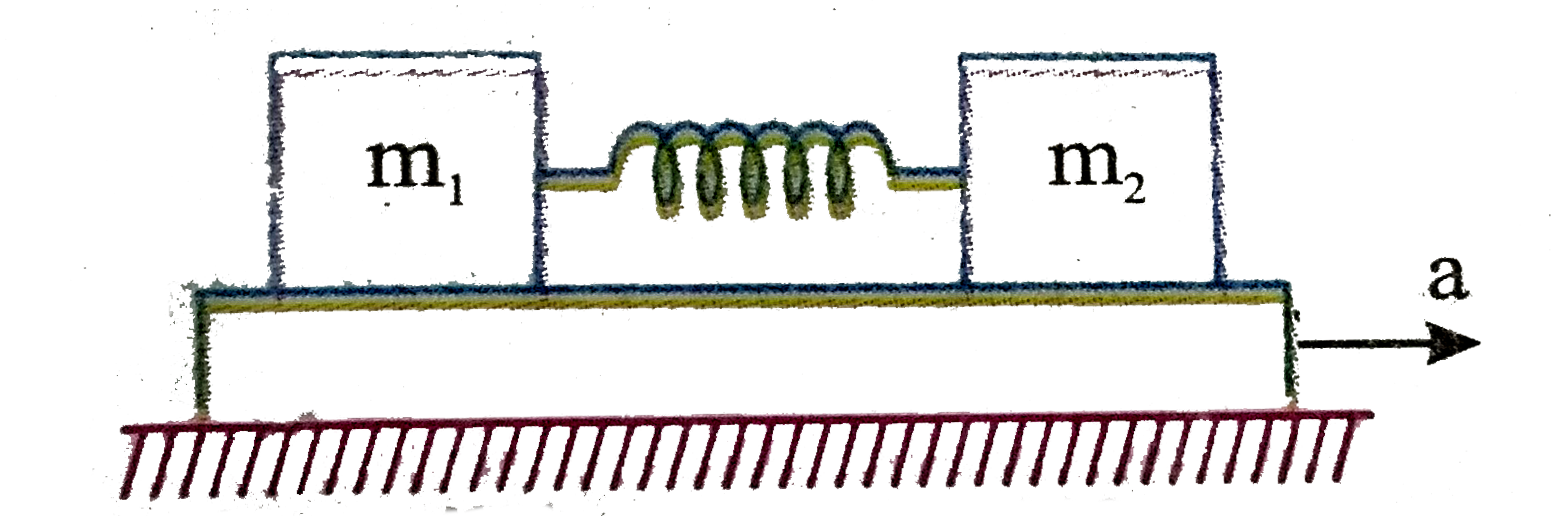 Aspring will be stretched if a>μgBspring will be commpressed if a≤μgCspring will neither be compressed nor be stretched for a<μg only.Dspring will be in its natural length under all conditions.
Aspring will be stretched if a>μgBspring will be commpressed if a≤μgCspring will neither be compressed nor be stretched for a<μg only.Dspring will be in its natural length under all conditions.A massive platform of mass M is moving with speed v=6ms−1 At t = 0, at body of mass m(m<<M) is gently placed on the platform. If c-efficient of friction between the body and platform is μ=0.3andg=10m/s2, then
Athe body covers a distance of 3 m on the platform in the direction of motion of the platform.Bthe body covers a distance of 3 m on the platform opposite to the direction of motion of the platform before coming to rest.Cthe body covers a distance of 6 m on the platform in the direction of motion of the platform.Dthe body covers a distance of 6 m on the platform opposite to the direction of motion of the platform before coming to rest.A block of mass mm remains stationary on a fixed inclined plane of inclination θ . If μ= coefficient of static friction the reaction of ground on the block is:
AμgcosθBmgcosθCmgsinθDmg↓
A mass of mass 60kg is pulling a mass M by an inextensible light rope passing through a smooth and massless pulley as shown in figure. The coefficient of friction between the mass and ground is μ=1/2 find the maximum value of M that can be pulled on the ground

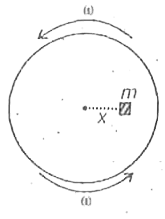
View SolutionA block of mass m is kept on horizontal turn table at x distance from the centre. If coefficient of friction between block and surface of turn table is μ, then maximum angular speed of the table so that block does not slip
View SolutionA rod AB of length 2m is hinging at point A and its other end B is attached to a platform on which a point of mass m is kept. Rod rotates about point A maintain angle θ=30∘ with the vertical in such a way that platform remain horizontal and revolves on the horizontal circular path. If the coefficient of static friction between the block and platform is μ=0.1 then find the maximum angular velocity in rads−1 of rod so that the block does not slip on the platform (g=10ms−2)
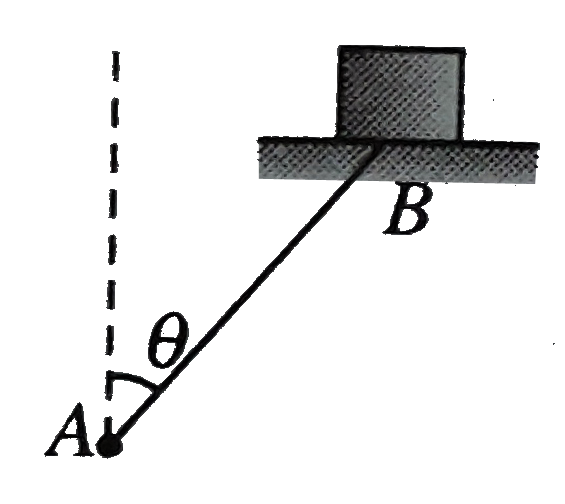
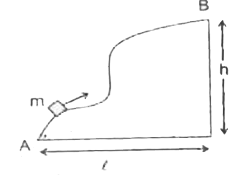
View SolutionA particle of mass m is pulled along an arbitrary curved surface without acceleration as shown in figure. Coefficient of friction between surface and particle is μ. Then

codes:
View SolutionA particle of mass m rotates with a uniform angular speed ω. It is viewed from a frame rotating about the Z-axis with a uniform angular speed ω0. The centrifugal force on the particler is
View Solution
