Find the centre of mass of a uniform semicircular ring of radius R and mass M.
Video Solution
Text Solution
Consider the centre of the ring at orign. Consider a differential element of length dl of the ring whose radius vector makes an angle θ with the x-axis. If the angle subtended by the length dl is dθ at the centre, then dl=Rdθ. Let λ be the mass per unit length. Then mass of this element is dm=λRdθ
⇒ycm=1m∫π0(Rsinθ)λRdθ=λR2m∫π0sinθdθ=λR2λπR[−cosθ]π0
⇒ycm=2R/π.

|
Topper's Solved these Questions
- COLLISION Book:FIITJEEChapter:COLLISION Exercise:SOLVED PROBLEMS (SUBJECTIVE)
Explore 10 Videos
- COLLISION Book:FIITJEEChapter:COLLISION Exercise:SOLVED PROBLEMS (OBJECTIVE)
Explore 18 Videos
- AC CIRCUITSBook:FIITJEEChapter:AC CIRCUITSExercise:ASSERTION REASONING TYPE
Explore 1 Video
- CURRENT ELECTRICITYBook:FIITJEEChapter:CURRENT ELECTRICITYExercise:Comprehension -4
Explore 3 Videos
Similar Questions
Knowledge Check
A particle of mass m is placed on centre of curvature of a fixed, uniform semi-circular ring of radius R and mass M as shown in figure. Calculate:
(a) interaction force between the ring and the particle and
(b) work required to displace the particle from centre of curvature to infinity.
 A(a)F=2GMπR2,(b)GMRB(a)F=2GMmπ2R,(b)GMmR2C(a)F=−2GMmπR2(b)−GMmRD(a)F=2GMmπR2(b)GMmR
A(a)F=2GMπR2,(b)GMRB(a)F=2GMmπ2R,(b)GMmR2C(a)F=−2GMmπR2(b)−GMmRD(a)F=2GMmπR2(b)GMmRConsider following statements
(1) CM of a uniform semicircular disc of radius R is 2R/π from the centre
(2) CM of a uniform semicircular ring of radius R is 4R/3π from the centre
(3) CM of a solid hemisphere of radius R is 4R/3π from the centre
(4) CM of a hemisphere shell of radius R is R/2 from the centre
Which statements are correct?A1, 2, 4B1, 3, 4C4 onlyD1, 2 only
Centre Of Mass Of Uniform Semi Circular Ring
View SolutionFind the centre of mass of a homogeneous semicircular plate of radius a.
View SolutionDetermine the centre of mass of a uniform hemisphere of radius R.
View SolutionLocate c.m. of thin , uniform semicircular wire of radius R.
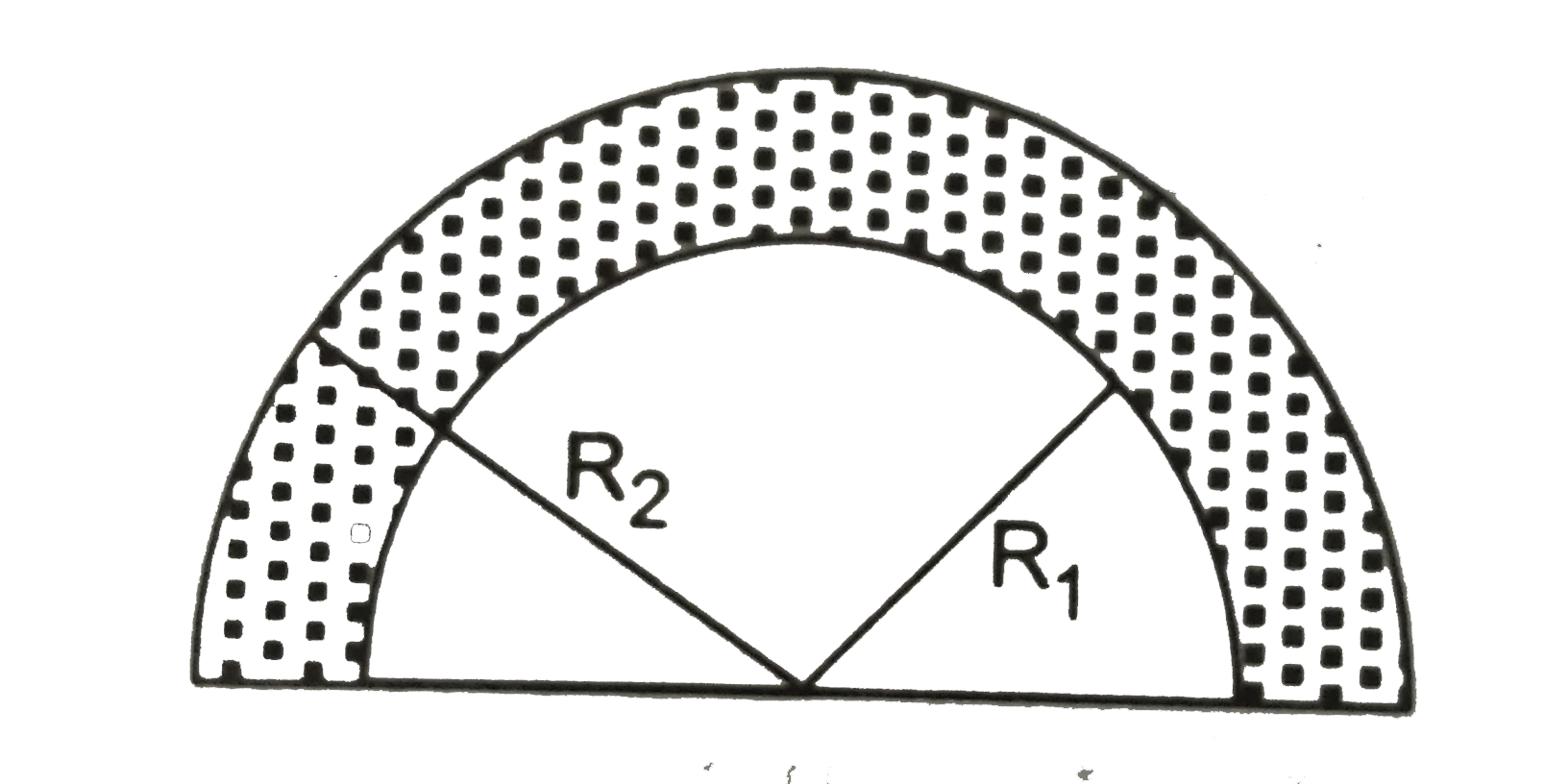
View SolutionFind the centre of mass of a uniform plate having semicircular inner and outer boundaries of radii R1andR2.
View SolutionFind the electric field at the centre of a uniformly charged semicircular ring of radius R. Linear charge density is λ
View Solution