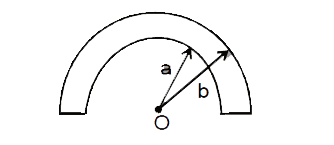
Find the centre of mass of a uniform plate having semicircular inner and outer boundaries of radii .
Video Solution
Text Solution
or
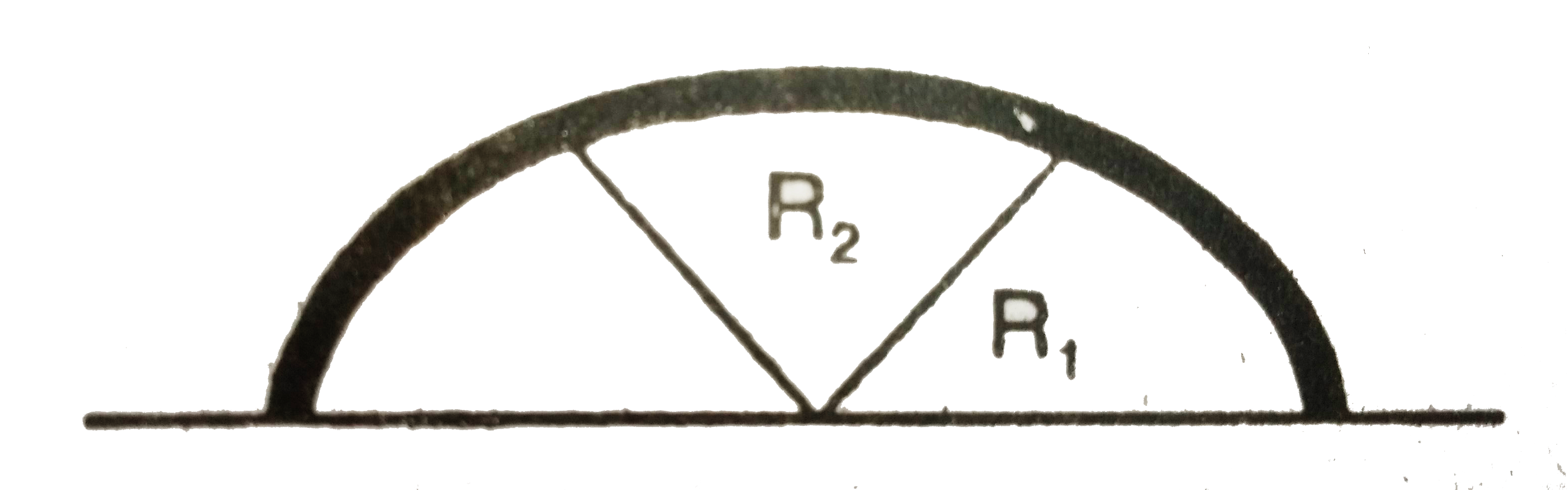
|
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBook:HC VERMAChapter:CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONExercise:Objective 2
Explore 11 Videos
- CALORIMETRYBook:HC VERMAChapter:CALORIMETRYExercise:Exercises
Explore 18 Videos
- CIRCULAR MOTIONBook:HC VERMAChapter:CIRCULAR MOTIONExercise:Exercises
Explore 30 Videos
Similar Questions
Knowledge Check
The moment of inertia of a uniform semicircular disc of mass disc through the centre is
A25Mr2B14Mr2C12Mr2DMr2Find the coordinates of centre of mass of a uniform semicircular closed wire frame with respect to the origin which is at its centre. Radius of the circular portion is R
 A(4R3π,0)B(2Rπ+2,0)C(2Rπ,0)D(Rπ+2,0)
A(4R3π,0)B(2Rπ+2,0)C(2Rπ,0)D(Rπ+2,0)In the figure shown, find out centre of mass of a system of a uniform circular plate of radius 3R from O in which a hole of radius R is cut whose centre is at 2R distance from the centre of large circular plate
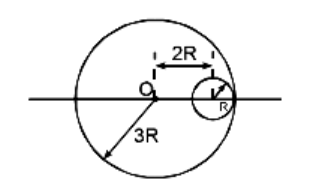 A(a) R2B(b) R5C(c) R4D(d) None of these
A(a) R2B(b) R5C(c) R4D(d) None of these
Find the centre of mass of a homogeneous semicircular plate of radius a.
View SolutionFind the location of centre of mass of a uniform semicirular plate of radius R and mass M.
View SolutionDetermine the centre of mass of a uniform hemisphere of radius R.
View SolutionFind the coordination of the centre of mass of a uniform semicircular wire of radius R and mass M.
View SolutionFind the centre of mass of a thin, uniform disc of radius R from which a small concentric disc of radius r is cut.
View Solution