Assume that a mango and its speed , both are spherical , now if the radius of seed is 25 of the thickness of the pulp . The seed lies exactly at the centre of the fruit . What percent of the total volume of the mango is its pulp ?
a. 6335%
b. 97.67%
c. 6823%
d. none of these
The correct Answer is:B
To solve the problem, we need to find the percentage of the total volume of the mango that is occupied by the pulp. We will follow these steps:
Step 1: Define the thickness of the pulp
Let the thickness of the pulp be denoted as x.
Step 2: Calculate the radius of the seed
According to the problem, the radius of the seed is given as 25 of the thickness of the pulp. Therefore, the radius of the seed rs can be calculated as:
rs=25x
Step 3: Calculate the radius of the mango
The radius of the mango rm is the sum of the thickness of the pulp and the radius of the seed:
rm=x+rs=x+25x=55x+25x=75x
Step 4: Calculate the volume of the seed
The volume Vs of a sphere is given by the formula:
V=43πr3
Thus, the volume of the seed is:
Vs=43π(25x)3=43π⋅8125x3=32375πx3
Step 5: Calculate the volume of the mango
Using the radius of the mango calculated earlier, the volume Vm of the mango is:
Vm=43π(75x)3=43π⋅343125x3=1372375πx3
Step 6: Calculate the volume of the pulp
The volume of the pulp Vp is the volume of the mango minus the volume of the seed:
Vp=Vm−Vs=1372375πx3−32375πx3=1340375πx3
Step 7: Calculate the percentage of the volume of the pulp
To find the percentage of the volume of the pulp with respect to the total volume of the mango, we use the formula:
Percentage of pulp=(VpVm)×100
Substituting the volumes we calculated:
Percentage of pulp=⎛⎝1340375πx31372375πx3⎞⎠×100=(13401372)×100
Step 8: Simplify and calculate the percentage
Calculating the above expression:
13401372≈0.9766
Thus,
Percentage of pulp≈97.66%
Conclusion
The percentage of the total volume of the mango that is its pulp is approximately 97.66%.
---
Let the thickness of the pulp be denoted as x.
According to the problem, the radius of the seed is given as 25 of the thickness of the pulp. Therefore, the radius of the seed rs can be calculated as:
rs=25x
The radius of the mango rm is the sum of the thickness of the pulp and the radius of the seed:
rm=x+rs=x+25x=55x+25x=75x
The volume Vs of a sphere is given by the formula:
V=43πr3
Thus, the volume of the seed is:
Vs=43π(25x)3=43π⋅8125x3=32375πx3
Using the radius of the mango calculated earlier, the volume Vm of the mango is:
Vm=43π(75x)3=43π⋅343125x3=1372375πx3
The volume of the pulp Vp is the volume of the mango minus the volume of the seed:
Vp=Vm−Vs=1372375πx3−32375πx3=1340375πx3
To find the percentage of the volume of the pulp with respect to the total volume of the mango, we use the formula:
Percentage of pulp=(VpVm)×100
Substituting the volumes we calculated:
Percentage of pulp=⎛⎝1340375πx31372375πx3⎞⎠×100=(13401372)×100
Calculating the above expression:
13401372≈0.9766
Thus,
Percentage of pulp≈97.66%
The percentage of the total volume of the mango that is its pulp is approximately 97.66%.
Topper's Solved these Questions
- MENSURATIONBOOK - ARIHANT SSCCHAPTER - MENSURATIONEXERCISE - TEST OF YOUR LEARNING
18 Videos
- MENSURATIONBOOK - ARIHANT SSCCHAPTER - MENSURATIONEXERCISE - EXERCISE (LEVEL 1)
55 Videos
- LOGARITHM BOOK - ARIHANT SSCCHAPTER - LOGARITHM EXERCISE - EXERCISE LEVEL 2
19 Videos
- MIXED GRAPHBOOK - ARIHANT SSCCHAPTER - MIXED GRAPHEXERCISE - Higher Skill Level Questions
15 Videos
Similar Questions
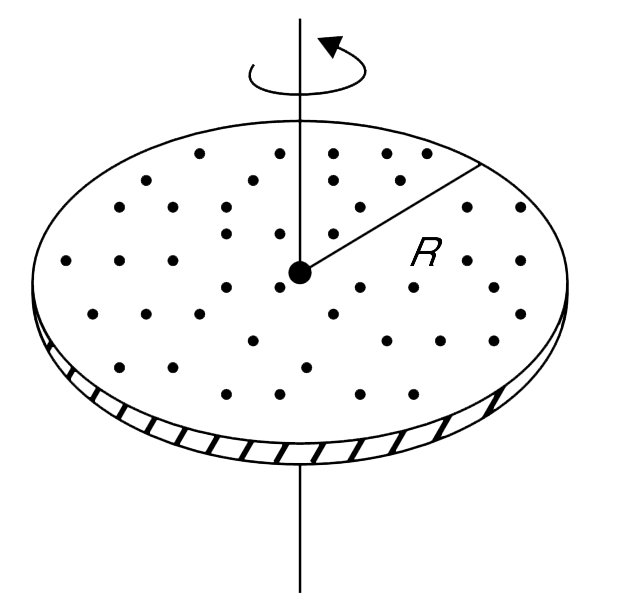
A metal disc of radius R can rotate about the vertical axis passing through its centre. The top surface of the disc is uniformly covered with dust particles. The disc is rotated with gradually increasing speed. At what value of the angular speed (ω) of the disc the 75%of the top surface will become dust free. Assume that the coefficient of friction between the dust particles and the metal disc is μ=0.5. Assume no interaction amongst the dust particles.
View SolutionA chain of length l is placed on a smooth spherical surface of radius R with one of its ends fixed at the top of the sphere. What will be the acceleration of the each element of the chain when its upper end is released? It is assumed that the length of the chain l<(πR2).
View Solution
Knowledge Check
Assume that a mango and its speed , both are spherical , now if the radius of seed is 25 of the thickness of the pulp . The seed lies exactly at the centre of the fruit . What percent of the total volume of the mango is its pulp ?
Aa. 6335%Bb. 97.67%Cc. 6823%Dd. none of theseThe total surface area of a cuboid is 392cm2 and the length of the cuboid is 12 cm. If the ratio of its breadth and its height is 8:5, then what is the volume of the cuboid?
A480cm3B1920cm3C3840cm3D20cm3
The total surface area of a cuboid is 392cm2 and the length of the cuboid is 12 cm. If the ratio of its breadth and its height is 8:5, then what is the volume of the cuboid?
View SolutionA chain of length l is placed on a smooth spherical surface of radius R with one of its ends fixed at the top of the sphere. What will be the acceleration w of each element of the chain when its upper end is released? It is assumed that the length of the chain l<12πR.
View SolutionWhile measuring the volume of a sphere , an error of 1.2% is commited in the measurement of radius . What percent error is introduced in the measurement of its volume ?
View SolutionThe total surface area of a cuboid is 392 cm2 and the length of the uboid is 12 cm. If the ratio of its breadth and height is 8:5 then what is the volume?
View SolutionA small sphere (emissivity=0.9,radius=r1) is located at the centre of a spherical asbestos shell (thickness=5.0 cm , outer radius =r2) The thickness of the shell is small compared to the inner and outer radii of the shell. The temperature of the small sphere is 800 K while the temperature of the inner surface of the shell is 600 K The temperature of small sphere is maintained constant. Assuming that r2r1=10.0 and ignoring any air inside the shell, find the temperature (in k) of the outer surface of the shell Take : Kasbes→r=0.085W/m∘ C σ=173×10−8W/m2k4
View SolutionOne circle has a radius of 5 and its centre at (0,5). A second circle has a radius of 12and its centre at (12,0). What is the length of a radius of a third circle which passes through the centre of the second circle and both the points of intersection of the first two circles.
View Solution
