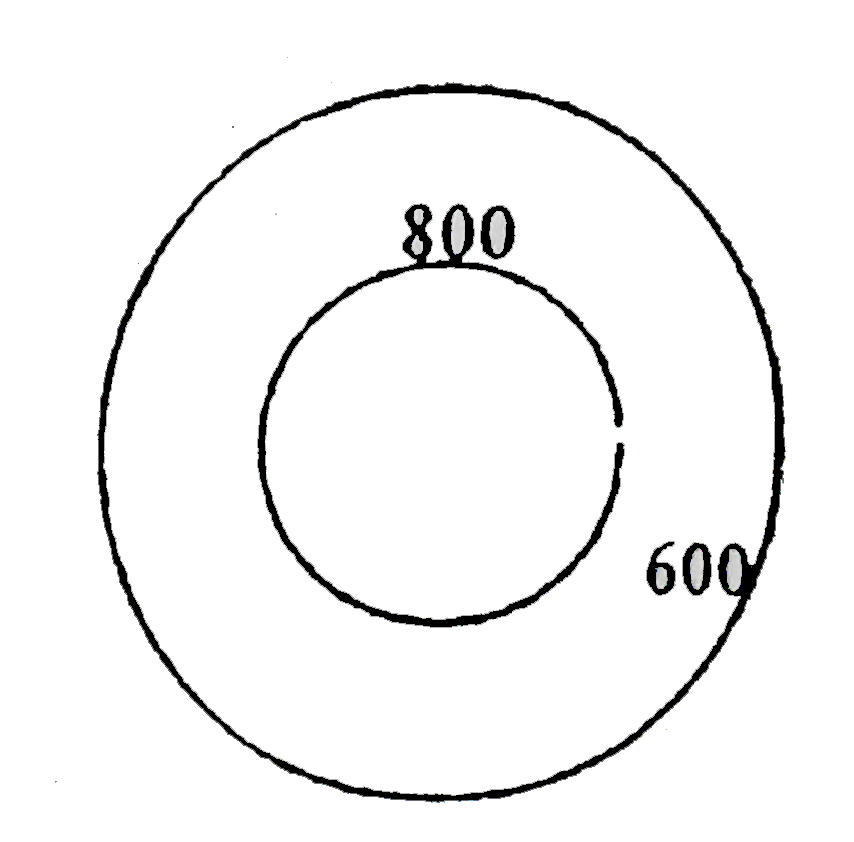
A small sphere (emissivity $= 0.9, r a d i u s = r_{1}$ ) is located at the centre of a spherical asbestos shell (thickness $= 5.0$ cm , outer radius $= r_{2}$ ) The thickness of the shell is small compared to the inner and outer radii of the shell. The temperature of the small sphere is 800 K while the temperature of the inner surface of the shell is 600 K The temperature of small sphere is maintained constant. Assuming that $\frac{r_{2}}{r_{1}} = 10.0$ and ignoring any air inside the shell, find the temperature (in k) of the outer surface of the shell Take : $K_{a s b e s \to r} = 0.085 W / m^{\circ}$ C $σ = \frac{17}{3} \times 10^{- 8} W / m^{2} k^{4}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $0516$

$\frac{d Q}{d t} = σ \times 0.8 \times 4 π r_{1}^{2} [800^{4} - 600^{4}]$
$= k \times \frac{4 π r_{2} r_{2}}{r_{2} - r_{2}} \times (600 - T)$
$r_{2} r_{2} \approx r_{2}^{2}$
$600 - T = \frac{\frac{17}{3} \times 10^{- 8} \times \frac{0.9}{10} \times \frac{1}{100} \times 10^{8} \times 100 \times 28 \times 10^{3} \times \frac{5}{100}}{0.085} \Rightarrow T = 516 K$

|

Updated on:21/07/2023

Class 12 PHYSICS MASTER PRACTICE PROBLEM

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A point source of heat of power P is placed at the centre of a thin spherical shell of a mean radius R. The material of the shell has thermal conductivity K. Calculate the thickness of the shell if the temperature difference between the outer and inner surfaces of the shell in steady - state is T.
A $\frac{4 π R^{2} K T}{2 P}$
B $\frac{3 π R^{4} K T}{P}$
C $\frac{4 π R^{2} K T}{P}$
D $\frac{2 π R^{2} K T}{3 P}$
Question 2 - Select One
Three concentric conducting spherical shells carry charges as : $+ 4 Q$ on the inner shell, $- 2 Q$ on the middle shell and $- 5 Q$ on the outer shell. The charge on the inner surface of the outer shell is
A0
B $4 Q$
C $- Q$
D $- 2 Q$
Question 3 - Select One
A solid spherical conducting shell has inner radius a and outer radius 2a. At the center of the shell is located a point charge $+ Q$ . What must the excess charge of the shell be in order for the charge density on the inner and outer surface of the shell to be exactly equal?

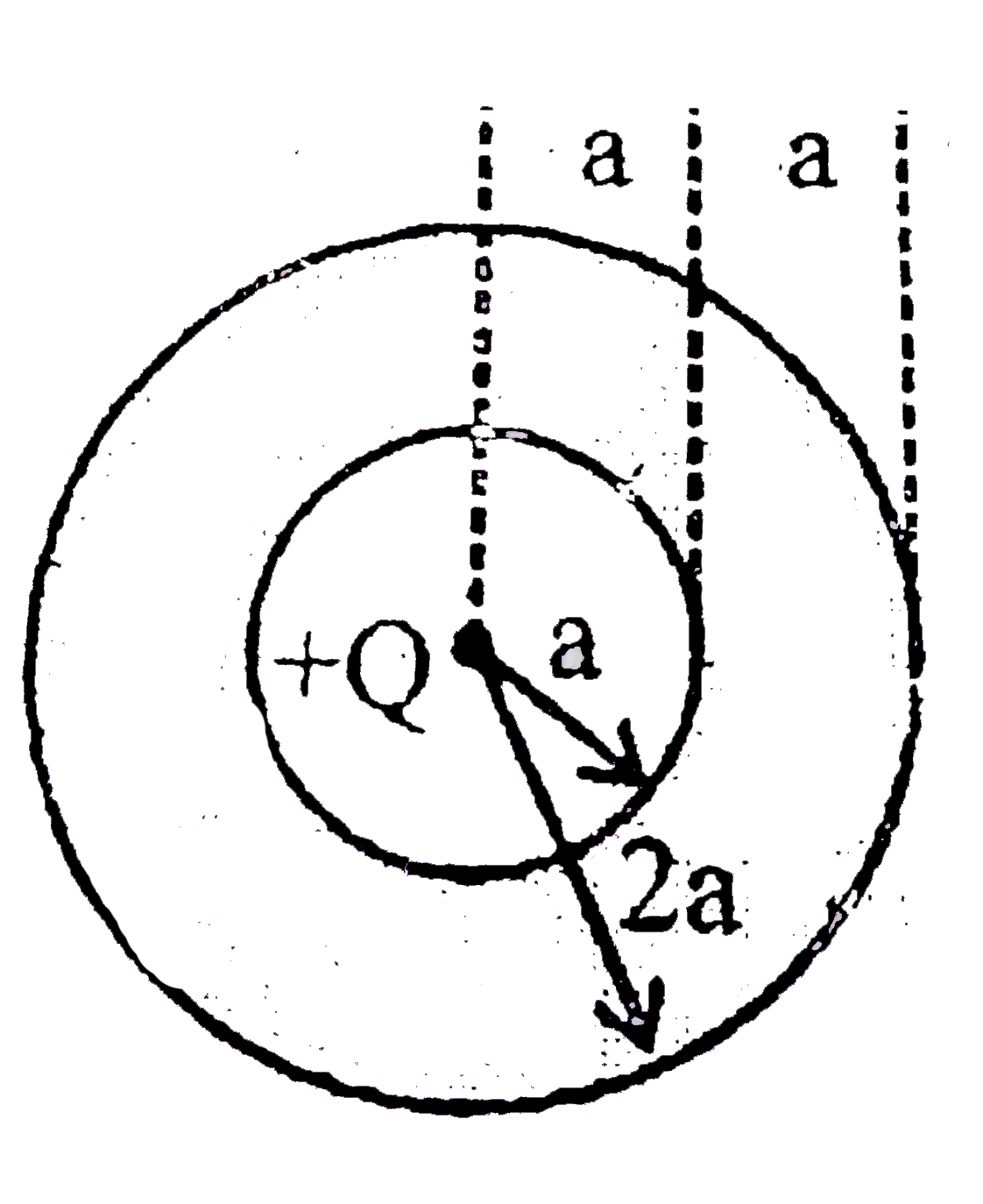A $- 5 Q$
B $+ 3 Q$
C $- 4 Q$
D $+ 4 Q$

BANSAL-MASTER PRACTICE PROBLEM-Subjective

Home
Ask Doubt
Profile