In a linear particle accelerator two large plane uniformly charged are placed parallel to each other as shown in the figure.
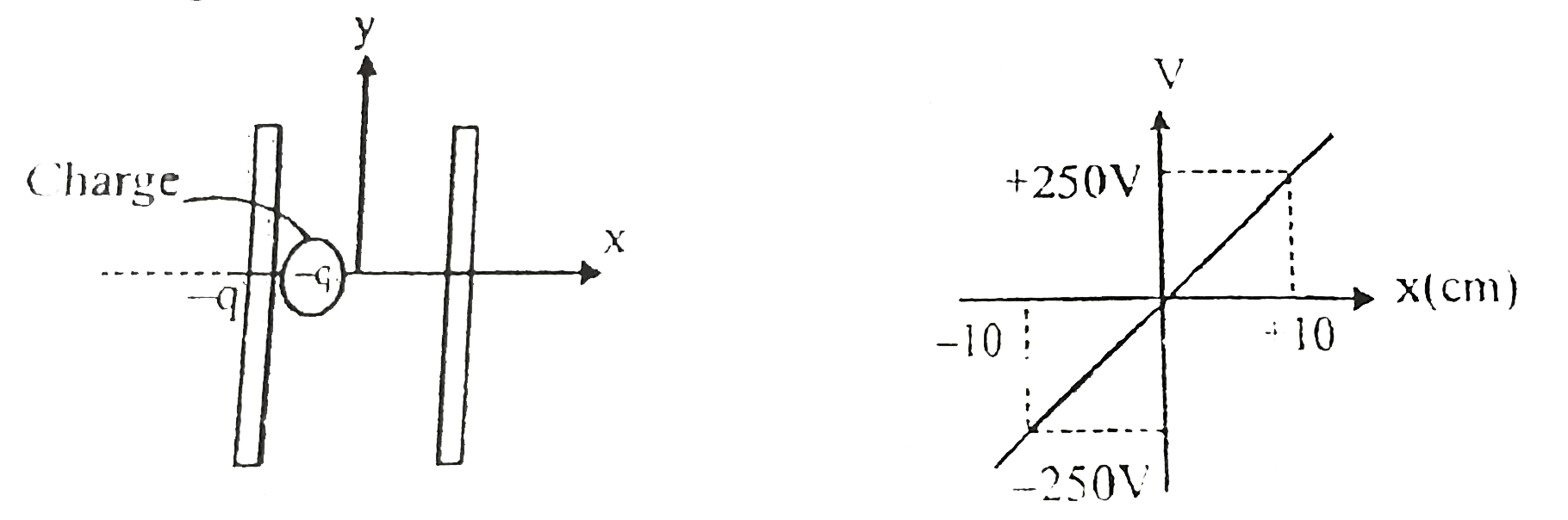
figure also shows variation of potential between planes A charged particle carrying a charge q=1.6×10−19 C and having mass m =16×10−31 kg is released from rest at x=−10 cm determine time taken (in ns ) by particle to strike the other plane Neglect relativistic considerations.
The correct Answer is:40
Electric field on particle E=E=−ΔVΔx=E=−[250−(−250)]20×10−2=−2500V/m
Acceleration of charge particle =qEm=1.6×10−19×250016×10−31)=2500×1011m/s2
thus time taken =√2×5a{S=12at2)
=√2×20×10−22500×1011=4×10−8sec=40nS
Topper's Solved these Questions
- MASTER PRACTICE PROBLEMBOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Additional topic
70 Videos
- MASTER PRACTICE PROBLEMBOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Multiple objective
131 Videos
- FLUID MECHANICSBOOK - BANSALCHAPTER - FLUID MECHANICSEXERCISE - PYQS AIEEE
10 Videos
- SEMICONDUCTORSBOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question
32 Videos
Similar Questions
The manifestation of band structure in solids is due to
View SolutionThe quantity// quantities that does //do not have mass in its// their dimentions (when we take standard 7 quantities as fundmental) is//are:
View SolutionA cylinder of height 20m is completely filled with water. The velocity of effux of water (∈ms−1) through a small hole on the side wall of the cylinder near its bottom is
View SolutionHow does the width of the depletion layer of a p-n junction diode change with decrease in reverse bias?
View SolutionAn infinte wire having linear charge density lambda is arranged as shown in fig. A charge particle of mass m and charge q is released charged q is released from point P. Find the initial acceleration of the particle just after the particle is released.
View SolutionTwo identical particles of mass m carry a charge Q, each. Initially one is at rest on a smooth horizontal plane and the other is projected along the plane directly towards first particle from a large distance with speed v. The closest distance of approach be .
View SolutionTwo infinitely long line charges having charge density lamda each are parallel to each other and separated by distance d. A charge particle of mass m and charge q is placed at mid point between them. This charge displaced slightly along a line AB which is perpendicular to the line charges and in the plane of the charges. prove that the motion of the particle will be SHM for small displacement and lamda q gt 0 Neglect gravity. Find the time period.
View SolutionA particle of mass 1.6xx10^(-27) kg and charge 1.6 xx 10^(-19) coulomb enters a uniform magnetic field of 1 Tesla as shown in the figure. The speed of the particle is 10^7 m//s . The distance PQ will be
View SolutionTwo charged particle of equal mass are constrained to move along X and Y direction. The X – Y plane is horizontal and the tracks are smooth. The particles are released from rest when they were at positions shown in the figure. At the instant distance of q becomes 2r from the origin, find the location of charge Q.

View SolutionTwo particle A and B (of masses m and 4m ) are released from rest in the two tunnels as shown in the figure-6.93. Which particle will cross the equatorial plane first?
View Solutionकिसी आवेशित कण का द्रवमान m तथा इस पर आवेश q हैं । कण को V विभवान्तर से त्वरित करने पर सम्बन्ध दी-ब्रोग्ली तरंगदैर्ध्य का सूत्र ज्ञात कीजिए ।
View SolutionThe electric field that can balance a charged particle of mass 3.2×10−27kg is (Given that the charge on the particle is 1.6×10−19C)
View SolutionThe velocity acquired by a charged particle of mass m and charge Q accelerated from rest by a potential of V is
View SolutionThe electric field that can balance a charged particle of mass 3.2xx10^(-27) kg is (Given that the charge on the particle is 1.6xx10^(-19)C )
View SolutionAn infinte wire having linear charge density lambda is arranged as shown in fig. A charge particle of mass m and charge q is released charged q is released from point P. Find the initial acceleration of the particle just after the particle is released.
View Solution
