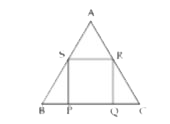
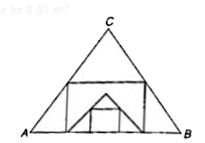
In the adjoining figure ABC is an equilateral triangle inscribeing a square of maximum possible area . Again in this square there is an equilateral triangle whose side is same as that of the square . Further the smaller equilateral triangle inscribes a square of maximum possible area . What is the area of the innermost square if the each side of the outermost triangle be 0.01 m ?
a. (873−504√3)cm2
b. (738−504√3)cm2
c. (873−405√2)cm2
d. none of these
The correct Answer is:A
Step by step video, text & image solution for In the adjoining figure ABC is an equilateral triangle inscribeing a square of maximum possible area . Again in this square there is an equilateral triangle whose side is same as that of the square . Further the smaller equilateral triangle inscribes a square of maximum possible area . What is the area of the innermost square if the each side of the outermost triangle be 0.01 m ? by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MENSURATIONBOOK - ARIHANT SSCCHAPTER - MENSURATIONEXERCISE - TEST OF YOUR LEARNING
18 Videos
- MENSURATIONBOOK - ARIHANT SSCCHAPTER - MENSURATIONEXERCISE - EXERCISE (LEVEL 1)
55 Videos
- LOGARITHM BOOK - ARIHANT SSCCHAPTER - LOGARITHM EXERCISE - EXERCISE LEVEL 2
19 Videos
- MIXED GRAPHBOOK - ARIHANT SSCCHAPTER - MIXED GRAPHEXERCISE - Higher Skill Level Questions
15 Videos
Similar Questions
Knowledge Check
Area of an equilateral triangle inscribed in a circle of radius a is
A√3a2/4Bπa2/3C3√3a2/4D√3πa2/4ABCD is a square and ABE is an equilateral triangle outside the square then
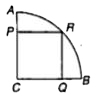
A∠ACE=12∠ABEB∠ACE=∠ABEC∠ACE=2∠ABEDNone of theseIn the adjoining figure a quadrant ( of circle ) inscribes a square of maximum possible area . If the radius of the circle be 'r' then what is the area of the square ?
 Ar22B3r25Cr2√3D2√6r
Ar22B3r25Cr2√3D2√6r
Prove that the area of equilateral triangle described on the side of a square is half the area of the equilateral triangle described on its diagonal.
View SolutionProve that the area of an equilateral triangle described on one side of a square is equal to half the area of the equilateral triangle described on one of its diagonals.
View SolutionThe ratio of the area of a square of side a and that of an equilateral triangle of side a, is
View SolutionThe area of a square and circle is same and the perimeter of square and equilateral triangle is same, then the ratio between the area of circle and the area of equilateral triangle is:
View SolutionAn equilateral triangle is described on the diagonal of a square. What is the ratio of the area of the triangle to that of the square? 2 :√3 (b) 4 :√3 (c) √3:2 (d) √3:4
View Solution