A cone whose height is 15 cm and radius of base is 6 cm is trimmed suficiently to reduce it to a pyramid whose base is an quilateral triangle . The volume of the portion removed is :
330cm3
328cm3
325cm3
331cm3
The correct Answer is:D
To solve the problem, we need to calculate the volume of the original cone and the volume of the pyramid formed after trimming. The volume of the portion removed will be the difference between these two volumes.
Step 1: Calculate the volume of the cone
The formula for the volume V of a cone is given by:
V=13πr2h
Where:
- r is the radius of the base
- h is the height
Given:
- Radius r=6 cm
- Height h=15 cm
Substituting the values into the formula:
V=13π(6)2(15)
Calculating (6)2:
(6)2=36
Now substituting back:
V=13π(36)(15)
Calculating 36×15:
36×15=540
So,
V=13π(540)=180π cm3
Step 2: Calculate the volume of the pyramid
The base of the pyramid is an equilateral triangle. The formula for the volume V of a pyramid is given by:
V=13×Base Area×Height
Step 2.1: Calculate the area of the equilateral triangle
The formula for the area A of an equilateral triangle with side length a is:
A=√34a2
To find the side length a of the equilateral triangle, we can use the radius of the circumcircle (which is the same as the radius of the cone's base). The radius r of the circumcircle of an equilateral triangle relates to its side length a as follows:
r=a√3
Given r=6 cm, we can find a:
6=a√3⟹a=6√3
Now substituting a into the area formula:
A=√34(6√3)2
Calculating (6√3)2:
(6√3)2=36×3=108
So,
A=√34×108=27√3 cm2
Step 2.2: Calculate the volume of the pyramid
Now we need the height of the pyramid. Since the cone is trimmed to form the pyramid, we can assume the height of the pyramid is the same as the height of the cone, which is 15 cm.
Now substituting the area of the base and height into the pyramid volume formula:
V=13×(27√3)×15
Calculating:
V=13×405√3=135√3 cm3
Step 3: Calculate the volume of the portion removed
The volume of the portion removed is the volume of the cone minus the volume of the pyramid:
Volume removed=Vcone−Vpyramid=180π−135√3
Final Answer
The volume of the portion removed is:
180π−135√3 cm3
- r is the radius of the base
- h is the height
- Radius r=6 cm
- Height h=15 cm
Topper's Solved these Questions
- MENSURATIONBOOK - ARIHANT SSCCHAPTER - MENSURATIONEXERCISE - EXERCISE (LEVEL 1)
55 Videos
- MENSURATIONBOOK - ARIHANT SSCCHAPTER - MENSURATIONEXERCISE - EXERCISE (LEVEL 2)
68 Videos
- MENSURATIONBOOK - ARIHANT SSCCHAPTER - MENSURATIONEXERCISE - INTRODUCTORY EXERCISE- 10.7
12 Videos
- LOGARITHM BOOK - ARIHANT SSCCHAPTER - LOGARITHM EXERCISE - EXERCISE LEVEL 2
19 Videos
- MIXED GRAPHBOOK - ARIHANT SSCCHAPTER - MIXED GRAPHEXERCISE - Higher Skill Level Questions
15 Videos
Similar Questions
Knowledge Check
A cone whose height is 15 cm and radius of base is 6 cm is trimmed suficiently to reduce it to a pyramid whose base is an quilateral triangle . The volume of the portion removed is :
A330cm3B328cm3C325cm3D331cm3A cone whose height is 24 cm and radius of base is 6 cm. The volume of the cone is :
A288πcu cmB144π cu cmC200 π cu cmD36π cu cm.From a solid cylinder whose height is 8 cm and radius is 6 cm, a conical cavity of height 8 cm and base radius 6 cm is hollowed out. Find the volume of the remaining solid.
A603cm3B720cm3C548cm3D637cm3
Find the volume of a pyramid whose base is a square of side 6 cm and height 20 cm.
View SolutionFrom a solid right circular cylinder with height 10 cm and radius of the base 6 cm, a right circular cone of the the same height and same base is removed . find the volume of the remaining solid
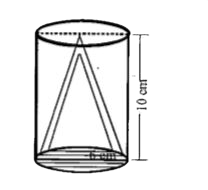
View SolutionFrom a solid right circular cylinder with height 10 cm and radius of the base 6 cm, a right circular cone of the same height and base is removed. Find the volume of the remaining solid. (Take π=3.14)
View SolutionFind the volume of the cone of height 10 cm and radius of the base 3 cm.
View SolutionFrom a solid cylinder of height 10 cm and radius of the base 6 cm, a cone of same height and same base is removed. The volume of the remaining solid is :
View Solution
