From a solid cylinder of height 10 cm and radius of the base 6 cm, a cone of same height and same base is removed. The volume of the remaining solid is :
240π cu. cm
5280 cu. cm
620π cu. cm
360π cu. cm
The correct Answer is:A
To find the volume of the remaining solid after removing a cone from a cylinder, we can follow these steps:
Step 1: Calculate the volume of the cylinder
The formula for the volume V of a cylinder is given by:
V=πr2h
Where:
- r is the radius of the base,
- h is the height of the cylinder.
Given:
- Radius r=6 cm,
- Height h=10 cm.
Substituting the values into the formula:
Vcylinder=π(62)(10)=π(36)(10)=360πcm3
Step 2: Calculate the volume of the cone
The formula for the volume V of a cone is given by:
V=13πr2h
Using the same radius and height as the cylinder:
Vcone=13π(62)(10)=13π(36)(10)=360π3=120πcm3
Step 3: Calculate the volume of the remaining solid
To find the volume of the remaining solid after the cone is removed from the cylinder, we subtract the volume of the cone from the volume of the cylinder:
Vremaining=Vcylinder−Vcone
Substituting the volumes we calculated:
Vremaining=360π−120π=240πcm3
Final Answer
The volume of the remaining solid is:
240πcm3
The formula for the volume V of a cylinder is given by:
- r is the radius of the base,
- h is the height of the cylinder.
- Radius r=6 cm,
- Height h=10 cm.
The formula for the volume V of a cone is given by:
To find the volume of the remaining solid after the cone is removed from the cylinder, we subtract the volume of the cone from the volume of the cylinder:
The volume of the remaining solid is:
Topper's Solved these Questions
- MENSURATIONBOOK - KIRAN PUBLICATIONCHAPTER - MENSURATIONEXERCISE - TYPE VI
47 Videos
- MENSURATIONBOOK - KIRAN PUBLICATIONCHAPTER - MENSURATIONEXERCISE - TYPE VII
60 Videos
- MENSURATIONBOOK - KIRAN PUBLICATIONCHAPTER - MENSURATIONEXERCISE - TYPE - IV
169 Videos
- LCM AND HCF BOOK - KIRAN PUBLICATIONCHAPTER - LCM AND HCF EXERCISE - Test Yourself
18 Videos
- MISCELLANEOUSBOOK - KIRAN PUBLICATIONCHAPTER - MISCELLANEOUSEXERCISE - TYPE-VI
15 Videos
Similar Questions
From a solid circular cylinder with height 10 cm and radius of the base 6 cm, a circular cone of the same height and same base is removed. Find the volume of remaining solid and also find the whole surface area.
View SolutionFrom a solid right circular cylinder with height 10 cm and radius of the base 6 cm, a right circular cone of the same height and base is removed. Find the volume of the remaining solid. (Take π=3.14)
View Solution
Knowledge Check
Assertion : From a solid cylinder whose height is 12 cm and diameter 10 cm a conical cavity of same height and same diameter is hollowed out. Volume of the cone is 2200 cm3.
Reason : If a conical cavity of same height and same diameter is hollowed out from a cylinder of height h and base radius r, then volume of the cone is equal to 1/2 of the 2 cylinder.AIf both assertion and reason are true and reason is the correct explanation of assertion.BIf both assertion and reason are true but reason is not the correct explanation of assertion.CIf assertion is true but reason is false.DIf assertion is false but reason is true.A cone whose height is 24 cm and radius of base is 6 cm. The volume of the cone is :
A288πcu cmB144π cu cmC200 π cu cmD36π cu cm.
From a solid right circular cylinder with height 10 cm and radius of the base 6 cm, a right circular cone of the the same height and same base is removed . find the volume of the remaining solid
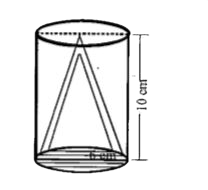
View SolutionFrom a right circular cylinder with height 10cm and radius of base 6cm, a right circular cone of the same height and base is removed. Find the volume of the remaining solid.
View SolutionFrom a solid cylinder of height 24 cm and radius 7 cm , a conical cavity of the same height and same radius is taken out . Find the volume of remaining solid .
View SolutionFind the volume of the cone of height 10 cm and radius of the base 3 cm.
View SolutionFrom a solid cylinder whose height is 8 cm and radius is 6 cm, a conical cavity of height 8 cm and base radius 6 cm is hollowed out, then volume of the remaining solid is
View SolutionFrom a solid circular cylinder with height 12 cm and radius of the base 5 cm, a right circular cone of the same height and the same base radius is removed find the volume and total surface area of the remaing solid . [User π=3.14]
View Solution