Question

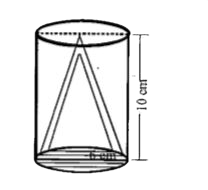
From a solid right circular cylinder with height 10 cm and radius of the base 6 cm, a right circular cone of the same height and base is removed. Find the volume of the remaining solid. (Take ${\displaystyle \pi =3.14}$)

Answer

`753.6 cm^(3)`

Explanation

To find the volume of the remaining solid after removing a right circular cone from a right circular cylinder, we will follow these steps:

Step 1: Identify the dimensions of the cylinder and cone
- Height of the cylinder (h) = 10 cm
- Radius of the base (r) = 6 cm

Step 2: Calculate the volume of the cylinder
The formula for the volume of a cylinder is given by:
\( V_{cylinder} = \pi r^2 h \)
Substituting the values:
\( V_{cylinder} = 3.14 \times (6)^2 \times 10 \)

Step 3: Calculate \(6^2\)
\( 6^2 = 36 \)

Step 4: Substitute \(6^2\) back into the volume formula
\( V_{cylinder} = 3.14 \times 36 \times 10 \)

Step 5: Calculate \(36 \times 10\)
\( 36 \times 10 = 360 \)

Step 6: Substitute back to find the volume of the cylinder
\( V_{cylinder} = 3.14 \times 360 \)

Step 7: Calculate \(3.14 \times 360\)
\( V_{cylinder} = 1130.4 \text{ cm}^3 \)

Step 8: Calculate the volume of the cone
The formula for the volume of a cone is given by:
\( V_{cone} = \frac{1}{3} \pi r^2 h \)
Substituting the values:
\( V_{cone} = \frac{1}{3} \times 3.14 \times (6)^2 \times 10 \)

Step 9: Substitute \(6^2\) into the cone volume formula
\( V_{cone} = \frac{1}{3} \times 3.14 \times 36 \times 10 \)

Step 10: Calculate the volume of the cone
Using the previously calculated \(36 \times 10 = 360\):
\( V_{cone} = \frac{1}{3} \times 3.14 \times 360 \)

Step 11: Calculate \(\frac{1}{3} \times 3.14 \times 360\)
First, calculate \(3.14 \times 360\):
\( 3.14 \times 360 = 1130.4 \)
Now divide by 3:
\( V_{cone} = \frac{1130.4}{3} = 376.8 \text{ cm}^3 \)

Step 12: Find the volume of the remaining solid
The volume of the remaining solid is given by:
\( V_{remaining} = V_{cylinder} - V_{cone} \)
Substituting the values:
\( V_{remaining} = 1130.4 - 376.8 \)

Step 13: Calculate the final volume
\( V_{remaining} = 753.6 \text{ cm}^3 \)

Final Answer
The volume of the remaining solid is \(753.6 \text{ cm}^3\).

---