Consider the polynomial f(x)=1+2x+3x2+4x3. Let s be the sum of all distinct real roots of f(x)and let t=|s|.
(−14,0)
(2164,1116)
(9,10)
(0,2164)
The correct Answer is:A
∫1/29f(x)dx<∫t0f(x)dx<∫3/40f(x)dx
Now, ∫f(x)dx=∫(1+2x+3x2+4x3)dx=x+x2+x3+x4
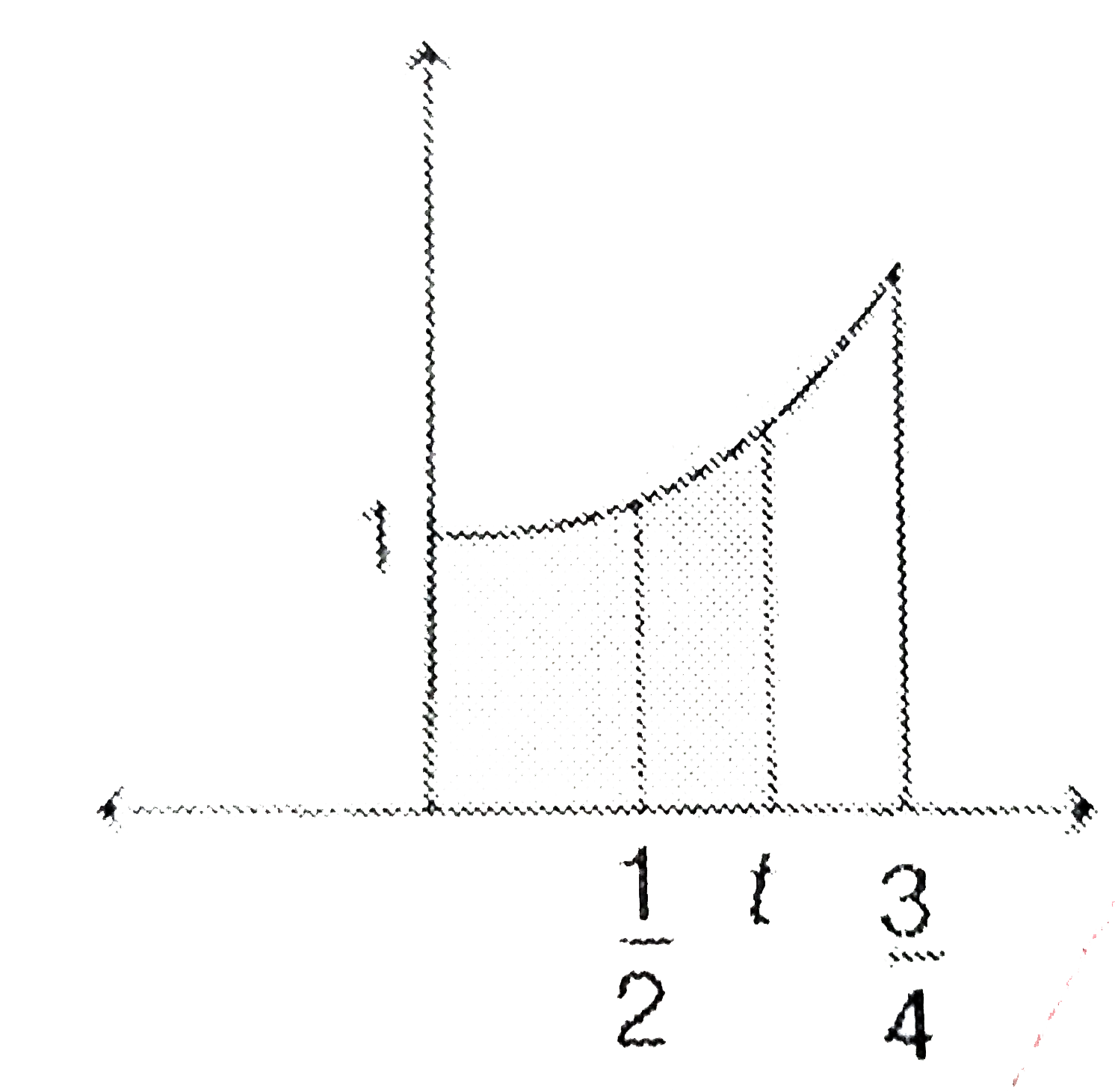
⇒∫1/20f(x)dx=1518>34,∫3/40f(x)dx=530256<3
Topper's Solved these Questions
- THEORY OF EQUATIONSBOOK - IIT JEE PREVIOUS YEARCHAPTER - THEORY OF EQUATIONSEXERCISE - GROPH OF QUADRATIC EXPRESSION
12 Videos
- STRAIGHT LINE AND PAIR OF STRAIGHT LINESBOOK - IIT JEE PREVIOUS YEARCHAPTER - STRAIGHT LINE AND PAIR OF STRAIGHT LINESEXERCISE - GENERAL EQUATION OF PAIR OF STRAIGHT LINES (Objective Questions I) (Only one correct option)
1 Videos
- TRIGONOMETRICAL EQUATIONSBOOK - IIT JEE PREVIOUS YEARCHAPTER - TRIGONOMETRICAL EQUATIONSEXERCISE - TOPIC 3 PROBLEMS BASED ON MAXIMUM AND MINIMUM OBJECTEIVE QUESTIONS I (ONLY ONE CORRECT OPTION)
9 Videos
Similar Questions
If f(x)=x3−3x+1, then the number of distinct real roots of the equation f(f(x))=0 is
View SolutionFor a polynomia g(x) with real coefficients, let mg denote the number of distinct real roots of g(x). Suppose S is the set of polynomials with real coefficients defined by
S={(x2−1)2(a0+a1+a2x2+a3x3):a0a1,a2,a3=R}
For a polynomial f. let f and f denote its first and second order derivties, respectively. Then the minimum possible value of (mf'+mf). where f∈S is, ____
View Solution
Knowledge Check
Let S be the set of all real roots of the equation 4x(4x−1)+2=|4x−1|+∣4x−2).Then S:
Ais an empty setBcontains at least four elementsCcontains exactly two elementsDis a singletonIf range of f(x)=x2−3x+2x2−ax+4 is R- (1) then sum of all possible real value(s) of 'a' is
A4B3C5DNone of theseLet f(x)=0 be a polynomial equation with real coefficients. Then between any two distinct real roots of f(x)=0, there exists at least one real root of the equation f'(x)=0. This result is a consequence of the celebrated Rolle's theorem applied to polynomials. Much information can be extracted about the roots of f(x)=0 from the roots of f'(x)=0.
If the roots of x3−12x+k=0 lie in (−4,−3),(0,1) and (2, 3), then the range of values of k isA4<k<11B9<k<11C8<k<13D4<k<13
Paragraph for Question Nos. 12 to 14 Consider f(x)=x3⋅(x−2)2⋅(x−1), then 12. The number of distinct real roots of equation f(x)=f(32) is (A) 2 (B) 3 (C)4 (D) 6 13. The number of distinct real roots of equation f(x)=f(23) (D)4 (C)3 (B) 2 (A) 1
View SolutionLet f(x) be a polynomial of degree 5 such that f(|x|)=0 has 8 real distinct , Then number of real roots of f(x)=0 is ________.
View SolutionLet f(x)=exx2 x∈R−{0}. If f(x) = k has two distinct real roots, then the range of k, is
View SolutionLet f(x)=(x+1)(x+2)(x+3)…..(x+100)andg(x)=f(x)f''(x)−f('(x))2. Let n be the numbers of rreal roots of g(x)=0, then:
View SolutionIf range of f(x)=x2−3x+2x2−ax+4 is R – {1} then sum of all possible real value(s) of 'a' is
View Solution
