Consider the parabola $y^{2} = 4 x$ , let P and Q be two points $(4, - 4)$ and $(9, 6)$ on the parabola. Let R be a moving point on the arc of the parabola whose x-coordinate is between P and Q. If the maximum area of triangle PQR is K, then ${(4 K)}^{1 / 3}$ is equal to

A

$\frac{125}{2}$

B

$\frac{75}{2}$

C

$\frac{625}{4}$

D

$\frac{125}{4}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

Given parabola is $y^{2} = 4 x,$
Since, X lies on the parabola, so let the fcoordinates of X be $(t^{2}, 2 t) .$ Thus the coordinates of the vertices of the traingle PXQ are $P (4, 4), x (t^{2} 2 t)$ and Q (9,6).

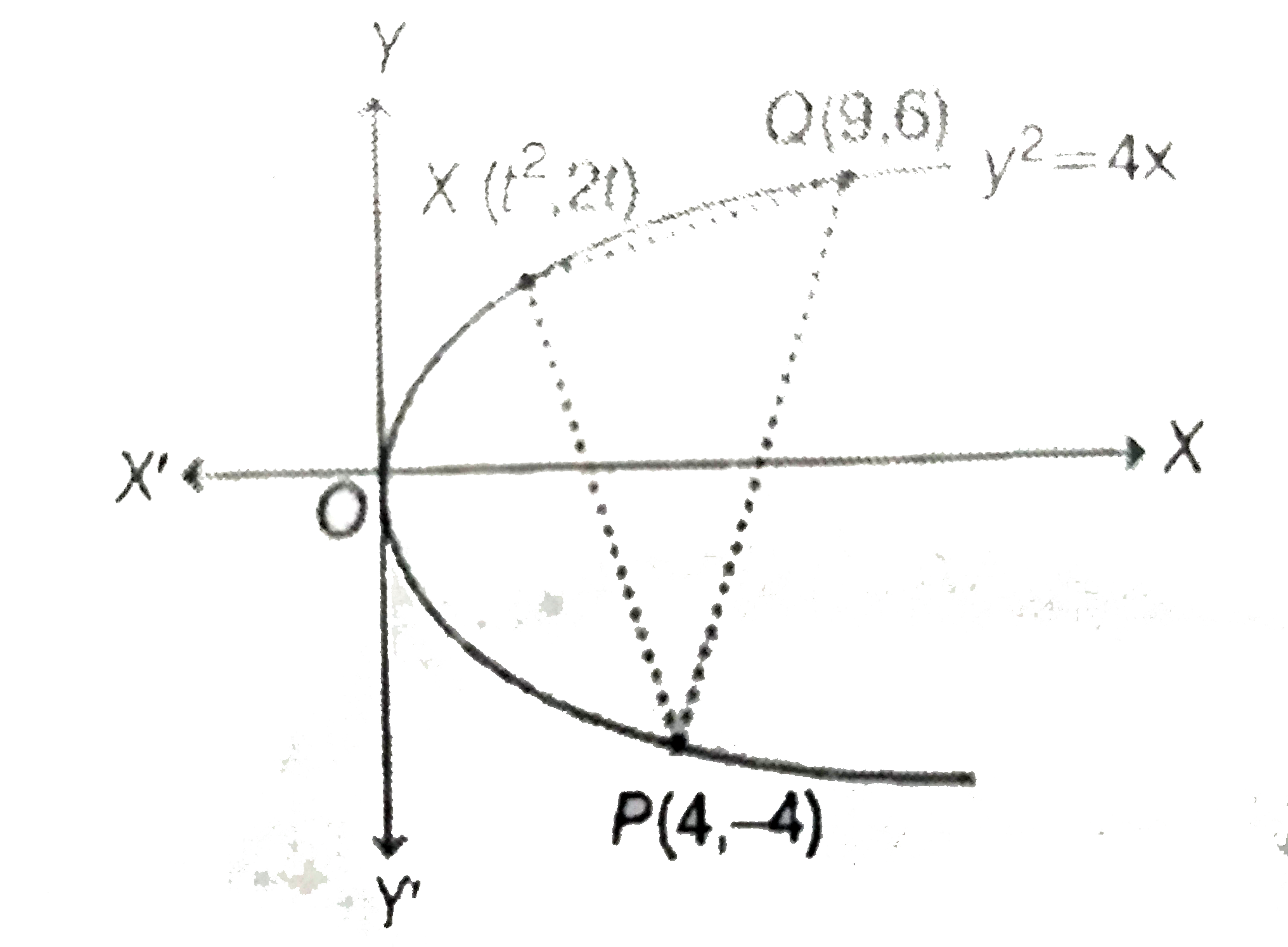
$∴ Area of Δ P X Q = \frac{1}{2} ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ \begin{matrix} 4 & - 4 & 1 t^{2} & 2 t & 1 9 & 6 & 1 \end{matrix} ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣ ∣$
$= \frac{1}{2} ∣ ∣ [4 (2 t - 6) + 4 (t^{2} 9 -) + 1 (6 t^{2} - 18 t)] ∣ ∣$
$= \frac{1}{2} ∣ ∣ [8 t - 24 + 4 t^{2} - 36 + 6 t^{2} - 18 t] ∣ ∣$
$= ∣ ∣ 5 t^{2} - 5 t - 30 ∣ ∣ = | 5 (t + 2) (t - 3) |$
Now, as X is any point on the are POQ of the parabola, therefore ordinate of point $X, 2 t \in (- 4, 6) \Rightarrow t \in (- 2, 3) .$
$∴ Area of Δ P X Q = - 5 (t + 2) (t - 3) = - 5 t^{2} + 5 t + 5 t + 30$
$[∵ | x - a | = - (x - a) . if x < a]$
The maximum area (in square units)
$= - [\frac{25 - 4 (- 5) (30)}{- (- 5)}] = \frac{125}{4}$
[ $∵$ Maximum value of quadratic expression $a x^{2} + b x + c, w h e n a < 0 i s - \frac{D}{4 α}]$

|

Updated on:21/07/2023

Class 12 MATHS QUADRATIC EQUATIONS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Let $P (4, - 4)$ and $Q (9, 6)$ be points on the parabola $y^{2} = 4 a (x - b)$ . Let R be a point on the arc of the parabola between P and Q. Then the area of $Δ P Q R$ is largest when.
A $∠ P R Q = \frac{π}{2}$
Bthe point R is $(4, 4)$
Cthe point R is $(\frac{1}{4}, 1)$
DNone of these
Question 2 - Select One
Let $A (4, - 4)$ and B(9,6) be points on the parabola $y^{2} = 4 x .$ Let C be chosen on the on the arc AOB of the parabola where O is the origin such that the area of $Δ A C B$ is maximum. Then the area (in sq. units) of $Δ A C B$ is :
A $30 . \frac{1}{2}$
B $31 . \frac{3}{4}$
C $31 . \frac{1}{4}$
D $32$
Question 3 - Select One
If the normals at two points P and Q of a parabola $y^{2} = 4 a x$ intersect at a third point R on the curve, then the product of ordinates of P and Q is (A) $4 a^{2}$ (B) $2 a^{2}$ (C) $- 4 a^{2}$ (D) $8 a^{2}$
A $4 a^{2}$
B $2 a^{2}$
C $- 4 a^{2}$
D $8 a^{2}$

IIT JEE PREVIOUS YEAR-THEORY OF EQUATIONS-GROPH OF QUADRATIC EXPRESSION

Home
Ask Doubt
Profile