Let $a, b, c$ be real. If $a x^{2} + b x + c = 0$ has two real roots $α a n d β, w h e r e α ⟨ - 1 a n d β ⟩ 1$ , then show that $1 + \frac{c}{a} + ∣ ∣ ∣ \frac{b}{a} ∣ ∣ ∣ < 0$

Video Solution

Text Solution

Verified by Experts

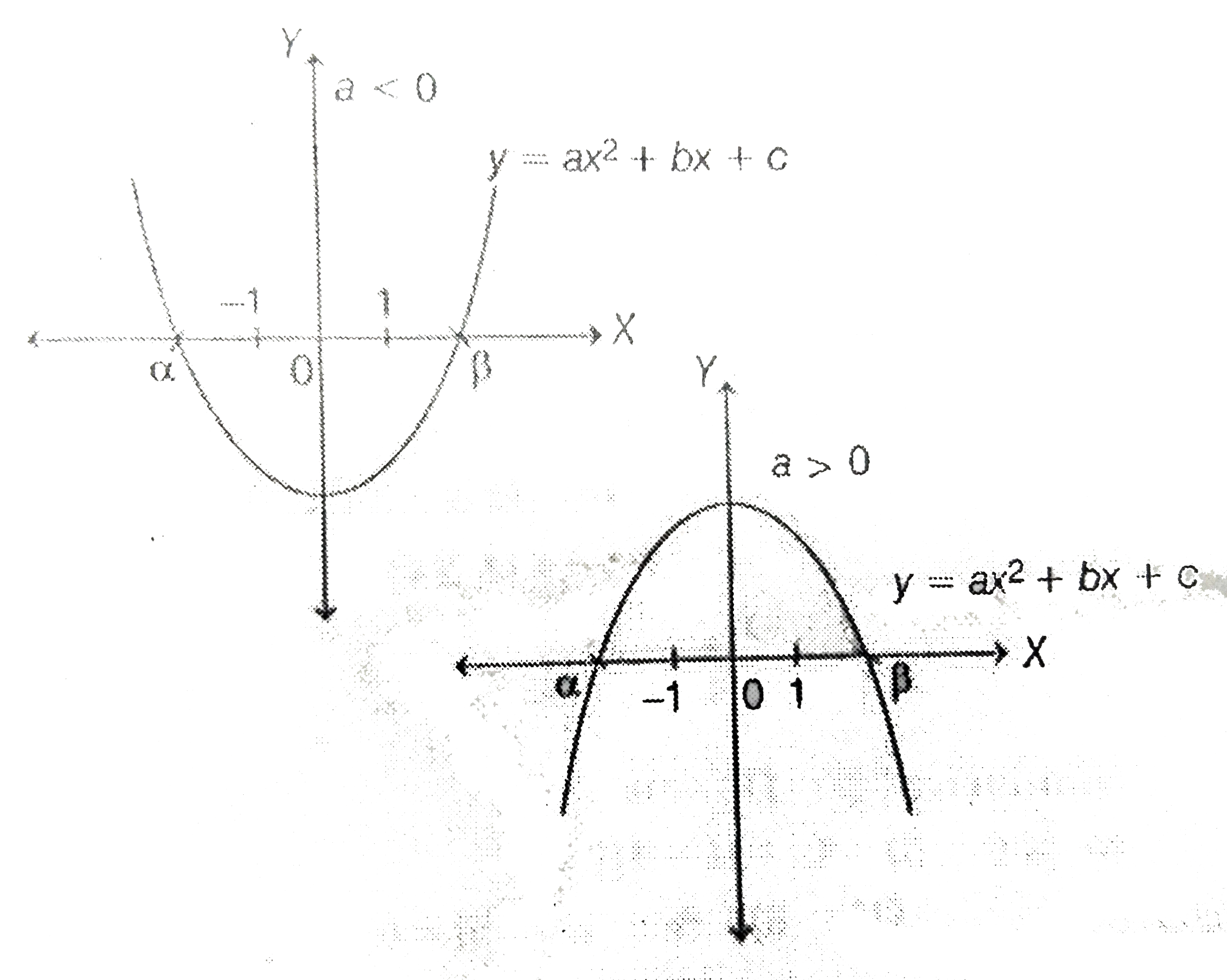
From figure it is clear that, if $a > 0,$ then $f (- 1) < 0 and f (1) < 0 and if a > 0, f (- 1) > 0 and f (1) > 0 .$ In both cases, $a f (- 1) < 0 and a f (1) < 0 .$
$\Rightarrow a (a - b + c) < 0 and a (a + b + c) < 0$
on dividing by $a^{2},$ we get
$1 - \frac{b}{a} + \frac{c}{a} < 0 and 1 + \frac{b}{a} + \frac{c}{a} < 0$
On combining both, we get
$1 \pm \frac{b}{a} + \frac{c}{a} < 0$
$\Rightarrow a + ∣ ∣ ∣ \frac{b}{a} ∣ ∣ ∣ + \frac{c}{a} < 0$

|

Updated on:21/07/2023

Class 12 MATHS QUADRATIC EQUATIONS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Let a, b, c be real, if $a x^{2} + b x + c = 0$ has two real roots $α, β,$ where $a < - 1 and β > 1$ , then the value of $1 + \frac{c}{a} + ∣ ∣ ∣ \frac{b}{a} ∣ ∣ ∣$ is :
Aless than zero
Bgreater than zero
Cequal to zero
Dequal to $b^{2} - 4 a c$
Question 2 - Select One
Let a, b, c be real, if $a x^{2} + b x + c = 0$ has two real roots $α, β,$ where $a < - 1 and β > 1$ , then the value of $1 + \frac{c}{a} + ∣ ∣ ∣ \frac{b}{a} ∣ ∣ ∣$ is :
Aless than zero
Bgreater than zero
Cequal to zero
Dequal to $b^{2} - 4 a c$
Question 3 - Select One
Let a, b, c be real, if $a x^{2} + b x + c = 0$ has two real roots $α, β,$ where $a < - 1 and β > 1$ , then the value of $1 + \frac{c}{a} + ∣ ∣ ∣ \frac{b}{a} ∣ ∣ ∣$ is :
Aa. less than -1
Bb. greater than zero
Cc. equal to zero
Dd. equal to $b^{2} - 4 a c$

IIT JEE PREVIOUS YEAR-THEORY OF EQUATIONS-GROPH OF QUADRATIC EXPRESSION

Home
Ask Doubt
Profile