Let S be the set of all non-zero numbers αsuch that the quadratic equation αx2−x+α=0has two distinct real roots x1,andx2 satisfying the inequality |x1−x2|<1 which of the following intervals is(are) a subset of S?
(−12,−1√5)
(−1√5,0)
(0,1√5)
(1√5,12)
The correct Answer is:A, D
Given,x1andx2 are roots of ax2−x+α=0.
∴x1+x2=1αandx1x2=1
Aslo,|x1−x2|<1
⇒|x1−x2|2<1⇒(x1−x2)2<1
or(x1+x2)2−4x1x2<1
⇒1α2−4<1or1α2<5
⇒5α2−1>0or(√5α−1)(√5α+1)>0
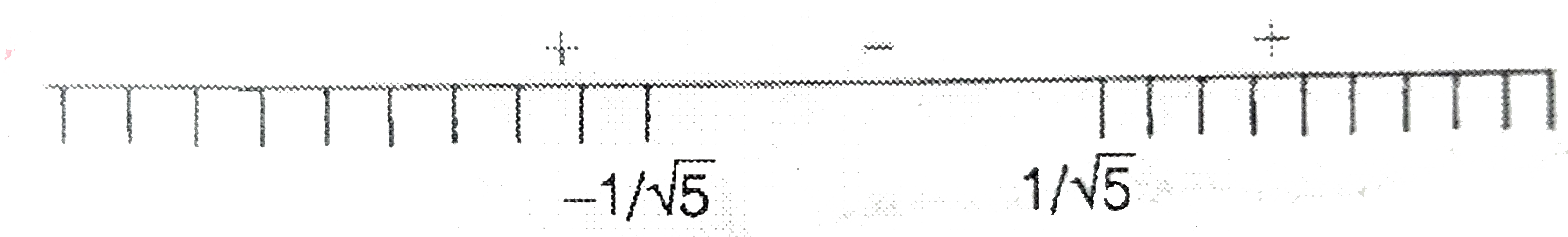
∴α∈(−∞o,−1√5)∪(1√5,∞) ...(i)
Also, ⇒1−4α2>0orα∈(−12,12) ...(ii)
From Eqs. (i) and ?(ii), we get
α∈(−12,−1√5)∪(1√5,12)
Topper's Solved these Questions
- THEORY OF EQUATIONSBOOK - IIT JEE PREVIOUS YEARCHAPTER - THEORY OF EQUATIONSEXERCISE - GROPH OF QUADRATIC EXPRESSION
12 Videos
- STRAIGHT LINE AND PAIR OF STRAIGHT LINESBOOK - IIT JEE PREVIOUS YEARCHAPTER - STRAIGHT LINE AND PAIR OF STRAIGHT LINESEXERCISE - GENERAL EQUATION OF PAIR OF STRAIGHT LINES (Objective Questions I) (Only one correct option)
1 Video
- TRIGONOMETRICAL EQUATIONSBOOK - IIT JEE PREVIOUS YEARCHAPTER - TRIGONOMETRICAL EQUATIONSEXERCISE - TOPIC 3 PROBLEMS BASED ON MAXIMUM AND MINIMUM OBJECTEIVE QUESTIONS I (ONLY ONE CORRECT OPTION)
9 Videos
Similar Questions
Let S be the set of all non-zero numbers αsuch that the quadratic equation αx2−x+α=0has two distinct real roots x1,andx2 satisfying the inequality |x1−x2|<1 which of the following intervals is(are) a subset of S?
View SolutionLet S be the set of all non-zero real numbers such that the quadratic equation αx2−x+α=0 has two distinct real roots x1andx2 satisfying the inequality |x1−x2|<1. Which of the following intervals is (are) a subset (s) of S? (12,1√5) b. (1√5,0) c. (0,1√5) d. (1√5,12)
View Solution
Knowledge Check
If quadratic equation f(x)=x2+ax+1=0 has two positive distinct roots then
Af(1)>0Bf′(1)<0Cf(0)−f′(0)=2Df′(0)<−2Let S be the set of all α∈R such that the equation, cos2x+αsinx=2α−7 has a solution. The S, is equal to
ARB[1,4]C[3,7]D[2,6]The real number k for which the equation 2x3+3x+k=0 has two distinct real roots in [0, 1]
Alies between 1 and 2Blies between 2 and 3Clies between -1 and 0Ddoes not exist
Let b be a non-zero real number. Suppose the quadratic equation 2x2+bx+1b= 0 has two distinct real roots. Then
View SolutionLet S be the set of all real values of α such that the second degree equation in x, x2−2αx+α2−2α−1=0 has two distinct real roots p and q satisfying condition 12(p−q)2−2(p+q)+2 is an integer, then number of elements in set S, is
View SolutionFind the value of K for which the quadratic equation kx2+2x+1=0,has real and distinct root.
View SolutionShow that there is no real number p for which the equation x2−3x+p=0 has two distinct roots in [0,1]
View SolutionThe set of values of α for which the quadratic equation (α+2)x2−2αx−α=0 has two roots on the number line symmetrically placed about the point 1 is
View Solution